题目内容
6.若分式-$\frac{{a}^{2}}{2a-6}$的值为正,则a的取值范围是a>3.若分式$\frac{x-1}{3-x}$的值为负数,则x应满足x>3或x<1.分析 根据分式的值,可得不等式,根据解不等式,可得答案.
解答 解:由分式-$\frac{{a}^{2}}{2a-6}$的值为正,得
-$\frac{{a}^{2}}{2a-6}$>0,解得a>3,
$\frac{x-1}{3-x}$<0,得$\frac{x-1}{x-3}$>0,
解得x>3或x<1.
故答案为:a>3;x>3或x<1.
点评 本题考查了分式的值,利用分式的值得出不等式解题关键.

练习册系列答案
相关题目
17.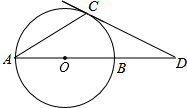 如图,AB是⊙O的直径,点C是⊙O上一点,过点C的切线与AB的延长线交于点D,连接AC、CO,若∠A=35°,则∠ADC的度数为( )
如图,AB是⊙O的直径,点C是⊙O上一点,过点C的切线与AB的延长线交于点D,连接AC、CO,若∠A=35°,则∠ADC的度数为( )
 如图,AB是⊙O的直径,点C是⊙O上一点,过点C的切线与AB的延长线交于点D,连接AC、CO,若∠A=35°,则∠ADC的度数为( )
如图,AB是⊙O的直径,点C是⊙O上一点,过点C的切线与AB的延长线交于点D,连接AC、CO,若∠A=35°,则∠ADC的度数为( )| A. | 20° | B. | 30° | C. | 35° | D. | 55° |
11.已知一次函数y=kx+b,当x=1时,y=-2,且它的图象与y轴交点纵坐标是-5,则它的解析式是( )
| A. | y=3x+5 | B. | y=-3x-5 | C. | y=-3x+5 | D. | y=3x-5 |
16.九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如表:
已知该运动服的进价为每件60元,设售价为x元.销量该运动服每件的利润为y元,销量为W件,其中W与x成一次函数关系.
(1)写出y与x的函数关系式;
(2)求出W与x的函数关系式;
(3)售价为150元时,月销售量是多少?
| 售价(元/件) | 100 | 110 | 120 | 130 | … |
| 月销量(件) | 200 | 180 | 160 | 140 | … |
(1)写出y与x的函数关系式;
(2)求出W与x的函数关系式;
(3)售价为150元时,月销售量是多少?
 在平面直角坐标系xOy中,对于点P(a,b)和点Q(a,b′),给出如下定义:
在平面直角坐标系xOy中,对于点P(a,b)和点Q(a,b′),给出如下定义: