题目内容
8．四边形ABCD中，AB=8，AD=6，BC=7.5，CD=10，AC=11，BD=13．在四边形ABCD内找一点O，使它到四边形四个顶点的距离之和最小，则其最小和为24．分析 要使四边形内存在一点，使它到四边形四个顶点的距离之和最小，这点就是四边形对角线的交点，由此得出答案即可．
解答 解：∵两点之间，线段最短，
∴在四边形ABCD内找一点O，使它到四边形四个顶点的距离之和最小，这个点O就是对角线的交点，
∵对角线AC=11，BD=13，
∴其最小和为11+13=24．
故答案为：24．
点评 此题考查线段的性质：两点之间，线段最短，把问题转化为求两条线段的和是解决问题的关键．
练习册系列答案
相关题目
19．下列实数：-$\frac{π}{4}$，0，$\sqrt{27}$，-$\frac{22}{7}$，$\root{3}{-\frac{1}{8}}$，-0.020020002…（每两个2之间依次增加一个0），其中是无理数的有（ ）
| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
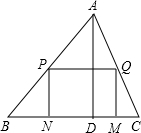一块材料的形状是锐角三角形ABC，边BC=12cm，高AD=8cm，把它加工成矩形零件如图，要使矩形的一边在BC上，其余两个顶点分别在AB，AC上．且矩形的长与宽的比为3：2，求这个矩形零件的边长．
3．
如图，在△ABC中，已知点D，E，F分别为边BC，AD，CE的中点，且S△ABC=8cm2，则S阴影等于（ ）
如图，在△ABC中，已知点D，E，F分别为边BC，AD，CE的中点，且S△ABC=8cm2，则S阴影等于（ ）| A． | 4cm2 | B． | 2cm2 | C． | 1cm2 | D． | 6cm2 |
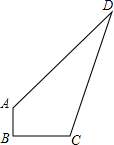某开发区有一空地ABCD，如图所示，现计划在空地上种草皮，经测量，∠B=90°，AB=3m，BC=4m，AD=13m，CD=12m，若每种植1平方米草皮需要150元，问总共需要投入多少元？
20．针对关于x的分式方程$\frac{m}{x+6}$=1．下列说法正确的是（ ）
| A． | 方程的解是x=m-6 | B． | m＞6时，方程的解是正数 | ||
| C． | m＜6时，方程的解为负数 | D． | 无法确定 |
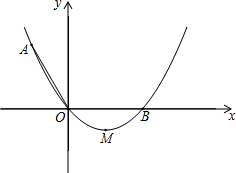如图，在平面直角坐标系xOy中，抛物线y=ax2+bx（a＞0）经过点A和x轴正半轴上的点B，顶点为M且AO=0B=2，∠AOB=120°．