题目内容
16.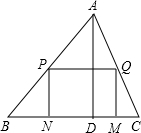 一块材料的形状是锐角三角形ABC,边BC=12cm,高AD=8cm,把它加工成矩形零件如图,要使矩形的一边在BC上,其余两个顶点分别在AB,AC上.且矩形的长与宽的比为3:2,求这个矩形零件的边长.
一块材料的形状是锐角三角形ABC,边BC=12cm,高AD=8cm,把它加工成矩形零件如图,要使矩形的一边在BC上,其余两个顶点分别在AB,AC上.且矩形的长与宽的比为3:2,求这个矩形零件的边长.
分析 根据矩形性质得PQ∥BC,PQ=MN,则可证明△APQ∽△ABC,根据相似的性质得出对应边成比例$\frac{PQ}{BC}=\frac{AH}{AD}$,分两种情况:①若PQ为长,PN为宽,设PQ=3k,PQ=2k;②PN为6,PQ为宽,设PN=3k,PQ=2k;分别由比例式得出方程,解方程即可.
解答 解:如图所示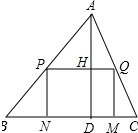
∵四边形PQMN是矩形,
∴BC∥PQ,
∴△APQ∽△ABC,
∴$\frac{PQ}{BC}=\frac{AH}{AD}$,
由于矩形长与宽的比为3:2,
∴分两种情况:
①若PQ为长,PN为宽,
设PQ=3k,PN=2k,
则$\frac{3k}{12}=\frac{8-2k}{8}$,
解得:k=2,
∴PQ=6cm,PN=4cm;
②PN为6,PQ为宽,
设PN=3k,PQ=2k,
则$\frac{2k}{12}=\frac{8-3k}{8}$,
解得:k=$\frac{24}{13}$,
∴PN=$\frac{72}{13}$cm,PQ=$\frac{48}{13}$cm;
综上所述:矩形的长为6cm,宽为4cm;或长为$\frac{72}{13}$cm,宽为$\frac{48}{13}$cm.
点评 本题考查了相似三角形的应用:在实际问题中抽象出几何图形,通过证明三角形相似,利用相似比表示线段之间的关系和计算线段的长.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11. 如图所示,点A为∠MON的角平分线上一点,过A任作一直线分别与∠MON的两边交于B、C,P为BC的中点,过P作BC的垂线交OA于点D.∠MON=50°,则∠BDC=( )
如图所示,点A为∠MON的角平分线上一点,过A任作一直线分别与∠MON的两边交于B、C,P为BC的中点,过P作BC的垂线交OA于点D.∠MON=50°,则∠BDC=( )
 如图所示,点A为∠MON的角平分线上一点,过A任作一直线分别与∠MON的两边交于B、C,P为BC的中点,过P作BC的垂线交OA于点D.∠MON=50°,则∠BDC=( )
如图所示,点A为∠MON的角平分线上一点,过A任作一直线分别与∠MON的两边交于B、C,P为BC的中点,过P作BC的垂线交OA于点D.∠MON=50°,则∠BDC=( )| A. | 120° | B. | 130° | C. | 140° | D. | 150° |
1.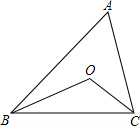 如图,△ABC中,∠A=50°,BO、CO分别是∠ABC、∠ACB的平分线,则∠BOC的度数是( )
如图,△ABC中,∠A=50°,BO、CO分别是∠ABC、∠ACB的平分线,则∠BOC的度数是( )
 如图,△ABC中,∠A=50°,BO、CO分别是∠ABC、∠ACB的平分线,则∠BOC的度数是( )
如图,△ABC中,∠A=50°,BO、CO分别是∠ABC、∠ACB的平分线,则∠BOC的度数是( )| A. | 115° | B. | 110° | C. | 105° | D. | 130° |
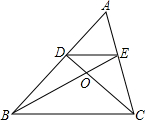 如图,已知点D、E分别在边AB、AC上,BE、CD交于点O,$\frac{AE}{AC}$=$\frac{DE}{BC}$=$\frac{EO}{BO}$.AC=5,EC=3,BC=6,BE=7
如图,已知点D、E分别在边AB、AC上,BE、CD交于点O,$\frac{AE}{AC}$=$\frac{DE}{BC}$=$\frac{EO}{BO}$.AC=5,EC=3,BC=6,BE=7