题目内容
3．
如图，在△ABC中，已知点D，E，F分别为边BC，AD，CE的中点，且S△ABC=8cm2，则S阴影等于（ ）| A． | 4cm2 | B． | 2cm2 | C． | 1cm2 | D． | 6cm2 |
分析 根据三角形的中线把三角形分成两个面积相等的三角形解答．
解答 解：∵点E是AD的中点，
∴S△ABE=$\frac{1}{2}$S△ABD，S△ACE=$\frac{1}{2}$S△ADC，
∴S△ABE+S△ACE=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×8=4，
∴S△BCE=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×8=4，
∵点F是CE的中点，
∴S△BEF=$\frac{1}{2}$S△BCE=$\frac{1}{2}$×4=2．
故选B．
点评 本题考查了三角形的面积，主要利用了三角形的中线把三角形分成两个面积相等的三角形，原理为等底等高的三角形的面积相等．
练习册系列答案
补充习题江苏系列答案
学练快车道口算心算速算天天练系列答案
相关题目
13．下列说法正确的是（ ）
| A． | a一定是正数，-a一定是负数 | B． | -1是最大的负整数 | ||
| C． | 0既没有倒数也没有相反数 | D． | 若a≠b，则a2≠b2 |
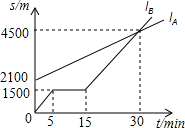A、B两名同学在一个学校上学，B同学上学的路上经过A同学家．A同学步行，B同学骑自行车，某天，A，B两名同学同时从家出发到学校，如图，lA表示A同学离B同学家的路程sA（m）与行走时间t（min）之间的函数关系图象，lB表示B同学离家的路程sB（m）与行走时间t（min）之间的函数关系图象．
11．
如图所示，点A为∠MON的角平分线上一点，过A任作一直线分别与∠MON的两边交于B、C，P为BC的中点，过P作BC的垂线交OA于点D．∠MON=50°，则∠BDC=（ ）
如图所示，点A为∠MON的角平分线上一点，过A任作一直线分别与∠MON的两边交于B、C，P为BC的中点，过P作BC的垂线交OA于点D．∠MON=50°，则∠BDC=（ ）| A． | 120° | B． | 130° | C． | 140° | D． | 150° |
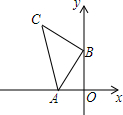如图，A（-2，0），B（0，4），以B点为直角顶点在第二象限作等腰直角△ABC，则C点坐标为（-4，6）．
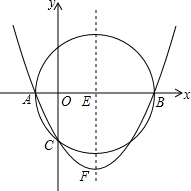如图，已知以E（3，0）为圆心，以5为半径的⊙E与x轴交于A，B两点，与y轴交于C点，抛物线y=ax2+bx+c经过A，B，C三点，顶点为F．