题目内容
9. 如图,菱形ABCD中,对角线AC、BD交于点O,E为AD边中点,菱形ABCD的周长为24,则OE的长等于( )
如图,菱形ABCD中,对角线AC、BD交于点O,E为AD边中点,菱形ABCD的周长为24,则OE的长等于( )| A. | 12 | B. | 6 | C. | 4 | D. | 3 |
分析 直接利用菱形的性质得出其边长以及对角线关系,进而利用直角三角形的性质得出EO的长.
解答 解:∵菱形ABCD的周长为24,
∴AD=6,∠AOD=90°,
∵E为AD边中点,
∴OE=3.
故选:D.
点评 此题主要考查了菱形的性质以及直角三角形的性质,正确掌握直角三角形的性质是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.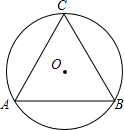 如图,等边△ABC是⊙O的内接三角形,则圆心O关于直线AB的对称点O′和⊙O的位置关系是( )
如图,等边△ABC是⊙O的内接三角形,则圆心O关于直线AB的对称点O′和⊙O的位置关系是( )
 如图,等边△ABC是⊙O的内接三角形,则圆心O关于直线AB的对称点O′和⊙O的位置关系是( )
如图,等边△ABC是⊙O的内接三角形,则圆心O关于直线AB的对称点O′和⊙O的位置关系是( )| A. | 在⊙O内 | B. | 在⊙O上 | C. | 在⊙O外 | D. | 不能确定 |
14. 二次函数y=ax2+bx+c(a≠0)如图所示,下列结论中:
二次函数y=ax2+bx+c(a≠0)如图所示,下列结论中:
①4ac-b2<0;
②3b+2c<0;
③4a+c<2b;
④m(am+b)+b<a(m≠-1).
其中正确的结论有( )
 二次函数y=ax2+bx+c(a≠0)如图所示,下列结论中:
二次函数y=ax2+bx+c(a≠0)如图所示,下列结论中:①4ac-b2<0;
②3b+2c<0;
③4a+c<2b;
④m(am+b)+b<a(m≠-1).
其中正确的结论有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
1.有五张正面分别写有数字-3,-2,1,2,3的卡片,它们的背面完全相同,现将这五张卡片背面朝上洗匀后随机抽取一张,以其正面的数字作为a的值,然后再从剩余的四张卡片中随机抽取一张,以其正面的数字作为b的值,则点(a,b)在第二象限的概率是( )
| A. | $\frac{3}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{10}$ | D. | $\frac{7}{10}$ |
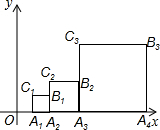 如图,正方形A1A2B1C1,A2A3B2C2,…Anan+1BnCn,如图位置依次摆放,已知点C1,C2,C3…,Cn在直线y=x上,点A1的坐标为(1,0).
如图,正方形A1A2B1C1,A2A3B2C2,…Anan+1BnCn,如图位置依次摆放,已知点C1,C2,C3…,Cn在直线y=x上,点A1的坐标为(1,0).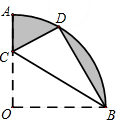 如图,在扇形OAB中,∠AOB=90°,半径OA=6.将扇形OAB沿过点B的直线折叠,点O恰好落在弧AB上点D处,折痕交OA于点C,则有下列选项:
如图,在扇形OAB中,∠AOB=90°,半径OA=6.将扇形OAB沿过点B的直线折叠,点O恰好落在弧AB上点D处,折痕交OA于点C,则有下列选项: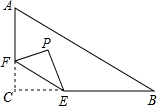 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是1.2.
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是1.2.