题目内容
14.某蛋糕产销公司A品牌产销线,2015年的销售量为9.5万份,平均每份获利1.9元,预计以后四年每年销售量按5000份递减,平均每份获利按一定百分数逐年递减;受供给侧改革的启发,公司早在2014年底就投入资金10.89万元,新增一条B品牌产销线,以满足市场对蛋糕的多元需求,B品牌产销线2015年的销售量为1.8万份,平均每份获利3元,预计以后四年销售量按相同的份数递增,且平均每份获利按上述递减百分数的2倍逐年递增;这样,2016年,A、B两品牌产销线销售量总和将达到11.4万份,B品牌产销线2017年销售获利恰好等于当初的投入资金数.(1)求A品牌产销线2018年的销售量;
(2)求B品牌产销线2016年平均每份获利增长的百分数.
分析 (1)根据题意容易得出结果;
(2)设A品牌产销线平均每份获利的年递减百分数为x,B品牌产销线的年销售量递增相同的份数为k万份;根据题意列出方程,解方程即可得出结果.
解答 解:(1)9.5-(2018-2015)×0.5=8(万份);
答:品牌产销线2018年的销售量为8万份;
(2)设A品牌产销线平均每份获利的年递减百分数为x,B品牌产销线的年销售量递增相同的份数为k万份;
根据题意得:$\left\{\begin{array}{l}{(9.5-0.5)+(1.8+k)=11.4}\\{(1.8+2k)•3(1+2x)^{2}=10.89}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=0.6}\\{x=5%}\end{array}\right.$,或$\left\{\begin{array}{l}{k=0.6}\\{x=-105%}\end{array}\right.$(不合题意,舍去),
∴$\left\{\begin{array}{l}{k=0.6}\\{x=5%}\end{array}\right.$,
∴2x=10%;
答:B品牌产销线2016年平均每份获利增长的百分数为10%.
点评 此题主要考查了一元二次方程的应用中平均变化率的方法.若设变化前的量为a,变化后的量为b,平均变化率为x,则经过两次变化后的数量关系为a(1±x)2=b.

练习册系列答案
相关题目
4.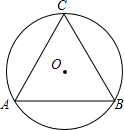 如图,等边△ABC是⊙O的内接三角形,则圆心O关于直线AB的对称点O′和⊙O的位置关系是( )
如图,等边△ABC是⊙O的内接三角形,则圆心O关于直线AB的对称点O′和⊙O的位置关系是( )
 如图,等边△ABC是⊙O的内接三角形,则圆心O关于直线AB的对称点O′和⊙O的位置关系是( )
如图,等边△ABC是⊙O的内接三角形,则圆心O关于直线AB的对称点O′和⊙O的位置关系是( )| A. | 在⊙O内 | B. | 在⊙O上 | C. | 在⊙O外 | D. | 不能确定 |
6.下列运算正确的是( )
| A. | a2•a3=a6 | B. | a5÷a2=a3 | C. | (-3a)3=-9a3 | D. | 2x2+3x2=5x4 |
3.下列各式计算正确的是( )
| A. | a2•a3=a6 | B. | (a2)3=a5 | C. | a2+3a2=4a4 | D. | a4÷a2=a2 |
13.超市招聘一名收银员,下面是三名应聘者各项测试成绩:
根据实际工作需要,该超市将计算机、商品知识和语言三项测试成绩按4:3:2的比例确定各人的素质测试成绩,三名应聘者中小赵将被录用.
| 素质测试 | 测试成绩/分 | ||
| 小李 | 小张 | 小赵 | |
| 计算机 | 80 | 70 | 85 |
| 商品知识 | 90 | 75 | 80 |
| 语言 | 85 | 80 | 95 |
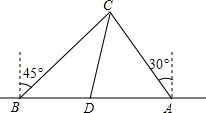 为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度,一天,我两艘海监船刚好在我某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍的船只停在C处海域.如图所示,AB=60($\sqrt{6}+\sqrt{2}$)海里,在B处测得C在北偏东45°的方向上,A处测得C在北偏西30°的方向上,在海岸线AB上有一灯塔D,测得AD=120($\sqrt{6}-\sqrt{2}$)海里.
为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度,一天,我两艘海监船刚好在我某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍的船只停在C处海域.如图所示,AB=60($\sqrt{6}+\sqrt{2}$)海里,在B处测得C在北偏东45°的方向上,A处测得C在北偏西30°的方向上,在海岸线AB上有一灯塔D,测得AD=120($\sqrt{6}-\sqrt{2}$)海里.