题目内容

18．计算：$\sqrt{（-2）^{2}}$-（$\frac{1}{3}$）-1+π0．

分析 直接利用二次根式的性质以及负整数指数幂的性质和零指数幂的性质分别化简求出答案．

解答 解：$\sqrt{（-2）^{2}}$-（$\frac{1}{3}$）-1+π0
=2-3+1
=0．

点评 此题主要考查了二次根式的性质以及负整数指数幂的性质和零指数幂的性质等知识，正确化简各数是解题关键．

练习册系列答案
相关题目
8．已知$\sqrt{a-1}$+$\sqrt{ab-2}$=0，
求$\frac{1}{ab}$+$\frac{1}{（a+1）（b+1）}$+$\frac{1}{（a+2）（b+2）}$+…+$\frac{1}{（a+2013）（b+2013）}$的值．
9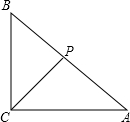．已知：Rt△ABC中，∠ACB=90°，CP平分∠ACB交边AB于点P，点D在边AC上．
（1）如果PD∥BC，求证：AC•CD=AD•BC；
（2）如果∠BPD=135°，求证：CP2=CB•CD．
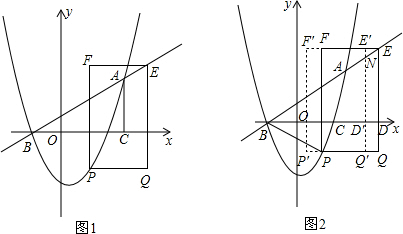
6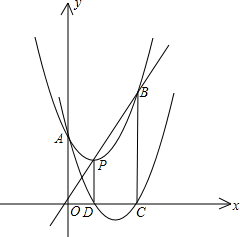．如图，抛物线F：y=ax2+bx+c的顶点为P，抛物线F与y轴交于点A，与直线OP交于点B，过点P作PD⊥x轴于点D，平移抛物线F使其经过点A，D得到抛物线F′：y=a′x2+b′x+c′，抛物线F′与x轴的另一个交点为C，若a，b，c满足b2=2ac，则四边形OABC的形状为（　　）
A．平行四边形B．正方形C．菱形D．矩形
13．下列计算正确的是（　　）
A．a3+a2=a5B．a4-a2=a2C．2a-3a=-aD．a5•a5=2a5
3．用代入法解下列方程组：
（1）$\left\{\begin{array}{l}{x=3y}\\{x+4y=14}\end{array}\right.$；
（2）$\left\{\begin{array}{l}{x-3=2y}\\{2x+1=3y}\end{array}\right.$；
（3）$\left\{\begin{array}{l}{3x-5y=6}\\{x+4y=-15}\end{array}\right.$；
（4）$\left\{\begin{array}{l}{2x-y=5}\\{3x+4y=2}\end{array}\right.$．
10．有甲、乙两个不透明的袋子中装着只有颜色不同的小球，甲袋中有两个红球，乙袋中有一个红球，一个白球，从两个袋中各摸出一个球，则两个球都是红球的概率是（　　）
A．$\frac{1}{2}$B．$\frac{1}{4}$C．$\frac{2}{3}$D．$\frac{1}{3}$
4．抛物线y=ax2+bx-3交x轴于B、C两点，且B的坐标为（-2，0）直线y=mx+n过点B和抛物线上另一点A（4，3）
（1）求抛物线和直线的解析式；
（2）若点P为抛物线上的一个动点，且在直线AB下方，过P作PQ∥x轴，且PQ=4（点Q在P点右侧）．以PQ为一边作矩形PQEF，且点E在直线AB上．求矩形PQEF的最大值．并求出此时点P的坐标；
（3）如图2，在（2）的结论下，连接AP、BP，设QE交于x轴于点D，现即将矩形PQEF沿射线DB以每秒1个单位长度的速度平移，当点D到达点B时停止，记平移时间为t，平移后的矩形PQEF为P′Q′E′F′，且Q′E′分别交直线AB、x轴于N、D′，设矩形P′Q′E′F′与△ABP的重叠部分面积为s，当NA=$\frac{\sqrt{5}}{8}$ND′时，求s的值．
5．已知（a-2）2+$\sqrt{b+3}$=0，则P（-a，-b）在（　　）
A．第一象限B．第二象限C．第三象限D．第四象限

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网