题目内容
6.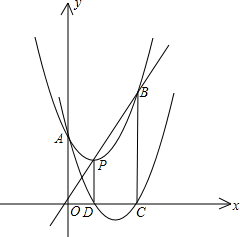 如图,抛物线F:y=ax2+bx+c的顶点为P,抛物线F与y轴交于点A,与直线OP交于点B,过点P作PD⊥x轴于点D,平移抛物线F使其经过点A,D得到抛物线F′:y=a′x2+b′x+c′,抛物线F′与x轴的另一个交点为C,若a,b,c满足b2=2ac,则四边形OABC的形状为( )
如图,抛物线F:y=ax2+bx+c的顶点为P,抛物线F与y轴交于点A,与直线OP交于点B,过点P作PD⊥x轴于点D,平移抛物线F使其经过点A,D得到抛物线F′:y=a′x2+b′x+c′,抛物线F′与x轴的另一个交点为C,若a,b,c满足b2=2ac,则四边形OABC的形状为( )| A. | 平行四边形 | B. | 正方形 | C. | 菱形 | D. | 矩形 |
分析 先表示出D的坐标,将D的坐标代入抛物线F′中,即可得出关于b,b′的关系式,根据抛物线F的解析式可求出P点的坐标,然后用待定系数法可求出OP所在直线的解析式.进而可求出抛物线F与直线OP的交点B的坐标,即可判断B的纵坐标与A点相同,则四边形OABC是矩形(∠AOC=90°).
解答 解:抛物线y=ax2+bx+c中,令x=0,则y=c,
∴A点坐标(0,c).
∵b2=2ac,
∴$\frac{4ac-{b}^{2}}{4a}$=$\frac{4ac-2ac}{4a}$=$\frac{2ac}{4a}$=$\frac{c}{2}$,
∴点P的坐标为(-$\frac{b}{2a}$,$\frac{c}{2}$).
∵PD⊥x轴于D,
∴点D的坐标为(-$\frac{b}{2a}$,0).
根据题意,得a=a′,c=c′,
∴抛物线F′的解析式为y=ax2+b'x+c.
又∵抛物线F′经过点D(-$\frac{b}{2a}$,0),
∴0=a×$\frac{{b}^{2}}{4{a}^{2}}$+b'(-$\frac{b}{2a}$)+c.
∴0=b2-2bb'+4ac.
又∵b2=2ac,
∴0=3b2-2bb'.
∴b:b′=2:3.
∴抛物线F′为y=ax2+$\frac{3}{2}$bx+c.
令y=0,则ax2+$\frac{3}{2}$bx+c=0.
∴x1=-$\frac{b}{2a}$,x2=-$\frac{b}{a}$.
∵点D的横坐标为-$\frac{b}{2a}$,
∴点C的坐标为(-$\frac{b}{a}$,0).
设直线OP的解析式为y=kx.
∵点P的坐标为(-$\frac{b}{2a}$,$\frac{c}{2}$),
∴$\frac{c}{2}$=-$\frac{b}{2a}$k,
∴k=-$\frac{2ac}{2b}$=-$\frac{{b}^{2}}{2b}$=-$\frac{b}{2}$,
∴y=-$\frac{b}{2}$x.
∵点B是抛物线F与直线OP的交点,
∴ax2+bx+c=-$\frac{b}{2}$x.
∴x1=-$\frac{b}{2a}$,x2=-$\frac{b}{a}$.
∵点P的横坐标为-$\frac{b}{2a}$,
∴点B的横坐标为-$\frac{b}{a}$.
把x=-$\frac{b}{a}$代入y=-$\frac{b}{2}$x,
得y=-$\frac{b}{2}$(-$\frac{b}{a}$)=$\frac{{b}^{2}}{2a}$.
∴点B的坐标为(-$\frac{b}{a}$,c).
∴BC∥OA,AB∥OC,
∴四边形OABC是平行四边形.
又∵∠AOC=90°,
∴四边形OABC是矩形.
故选D.
点评 本题着重考查了待定系数法求二次函数的性质、函数的平移变换、探究矩形的构成情况等重要知识点,函数图象的平移问题,弄清楚抛物线在平移过程中,各系数的变化情况是本题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | 由a>b得-2a>-2b | B. | 由-1>-2得$\frac{1}{\sqrt{2}}$>$\frac{2}{\sqrt{2}}$ | C. | 由a>b得ac>bc | D. | 由a>b得-a<-b |

| A. |  | B. |  | C. |  | D. |  |
| A. | -3 | B. | 1 | C. | 0 | D. | 2 |
| A. | (-2)2 | B. | -$\sqrt{2}$ | C. | $\frac{1}{2}$ | D. | -(-1) |