题目内容
14.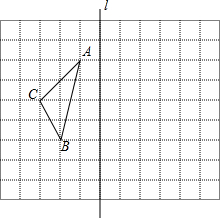 如图所示的方格纸中,每一个小正方形的边长都是1,网格中有一个格点三角形ABC.
如图所示的方格纸中,每一个小正方形的边长都是1,网格中有一个格点三角形ABC.(1)以直线l为对称轴,在图中直接作出△ABC的轴对称图形△A′B′C′.
(2)在直线l右侧,在△A′B′C′外部,画出以B′C′为腰的一个等腰直角三角形DB′C′.
(3)计算△DB′C′的面积,并通过面积求出B′C′的长度.
分析 (1)直接利用轴对称图形的性质得出对应点位置进而得出答案;
(2)利用等腰直角三角形的性质得出答案;
(3)直接利用三角形面积结合等腰直角三角形的性质得出答案.
解答  解:(1)如图所示:△A′B′C′,即为所求;
解:(1)如图所示:△A′B′C′,即为所求;
(2)如图所示:等腰直角三角形DB′C′和△D′B′C′,即为所求;
(3)△DB′C′的面积为:S=2×3-$\frac{1}{2}$×1×2-$\frac{1}{2}$×1×2-$\frac{1}{2}$×1×3=$\frac{5}{2}$,
∵$\frac{1}{2}$B′C′2=$\frac{5}{2}$,
∴B′C′=$\sqrt{5}$.
点评 此题主要考查了轴对称变换以及三角形面积求法,正确得出对应点位置是解题关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
2. 如图,把直线l沿x轴正方向向右平移2个单位得到直线l′,则直线l′的解析式为( )
如图,把直线l沿x轴正方向向右平移2个单位得到直线l′,则直线l′的解析式为( )
 如图,把直线l沿x轴正方向向右平移2个单位得到直线l′,则直线l′的解析式为( )
如图,把直线l沿x轴正方向向右平移2个单位得到直线l′,则直线l′的解析式为( )| A. | y=2x+4 | B. | y=-2x-2 | C. | y=2x-4 | D. | y=-2x-2 |
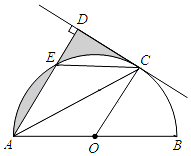 如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB如图,AB是
如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB如图,AB是 在如图的网格图中,每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=4.
在如图的网格图中,每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=4. 如图,在△ABC中,∠C=90°,AC=6,BC=8,D、E分别是斜边AB和直角边CB上的点,把△ABC沿着直线DE折叠,使顶点B的对应点B′落在直角边AC的中点上,求CE的长.
如图,在△ABC中,∠C=90°,AC=6,BC=8,D、E分别是斜边AB和直角边CB上的点,把△ABC沿着直线DE折叠,使顶点B的对应点B′落在直角边AC的中点上,求CE的长.