Question

5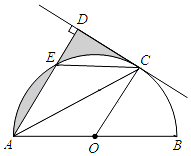．如图，AB是⊙O的直径，C是半圆O上的一点，AC平分∠DAB如图，AB是
⊙O的直径，C是半圆O上的一点，AC平分∠DAB，AD⊥CD，垂足为D，AD交⊙O于E，连接CE．
（1）判断CD与⊙O的位置关系，并证明你的结论；
（2）若E是弧AC的中点，⊙O的半径为1，求图中阴影部分的面积．

Answer 1

分析 （1）CD与圆O相切，理由如下：由AC为角平分线得到一对角相等，利用等角对等边得到一对角相等，等量代换得到一对内错角相等，利用内错角相等两直线平行得到OC与AD平行，进而得到OC与CD垂直，即可得证；
（2）连接EB，交OC于F，利用直径所对的圆周角为直角，以及切线的性质，得到一对直角相等，利用同位角相等两直线平行得到OC与AD平行，由O为AB中点，得到F为BE中点，利用中位线定理求出OF的长，进而利用勾股定理求出EF的长，阴影部分面积等于三角形EDC面积，求出即可．

解答 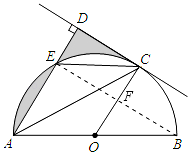解：（1）CD与圆O相切，理由如下：
∵AC为∠DAB的平分线，
∴∠DAC=∠BAC，
∵OA=OC，
∴∠OAC=∠OCA，
∴∠DAC=∠OCA，
∴OC∥AD，
∵AD⊥CD，
∴OC⊥CD，
则CD与圆O相切；                                
（2）连接EB，交OC于F，
∵E为弧AC的中点，
∴$\widehat{AE}$=$\widehat{CE}$，
∴AE=EC，
∴∠EAC=∠ECA，
∵AC为∠DAB平分线，
∴∠EAC=∠CAO，
∵OA=OC，
∴∠OAC=∠OCA，
∴∴∠EAC=∠OCA，∠ECA=∠CAO，
∴AE∥OC，EC∥AO，
∴四边形AECO为平行四边形，
∵OA=OC，
∴四边形AECO为菱形，
∴AE=OA=1，
∵AB为直径，
∴∠AEB=90°，
∴EB∥CD，
∵CD与⊙O相切，C为切点，
∴OC⊥CD，
∴OC∥AD，
∵点O为AB的中点，
∴OF为△ABE的中位线，
∴OF=$\frac{1}{2}$AE=$\frac{1}{2}$，即CF=DE=$\frac{1}{2}$，
在Rt△OBF中，根据勾股定理得：EF=FB=DC=$\frac{\sqrt{3}}{2}$，
则S_阴影=S_△DEC=$\frac{1}{2}$×$\frac{1}{2}$×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{8}$．

点评 此题考查了直线与圆的位置关系，角平分线性质，以及扇形面积求法，熟练掌握切线的性质是解本题的关键．