题目内容
9．（1）计算：（$\sqrt{2}$+1）-$\sqrt{2}$tan45°+|-$\sqrt{2}$|；（2）解方程：x2-2$\sqrt{3}$x+3=0．
分析 （1）先将三角函数值代入，再根据实数的混合运算顺序计算可得；
（2）因式分解法求解可得．
解答 解：（1）原式=$\sqrt{2}$+1-$\sqrt{2}$×1+$\sqrt{2}$
=$\sqrt{2}$+1-$\sqrt{2}$+$\sqrt{2}$
=$\sqrt{2}$+1；
（2）∵（x-$\sqrt{3}$）2=0，
∴x-$\sqrt{3}$=0，
即x1=x2=$\sqrt{3}$．
点评 本题主要考查解一元二次方程的能力，熟练掌握解一元二次方程的几种常用方法：直接开平方法、因式分解法、公式法、配方法，结合方程的特点选择合适、简便的方法是解题的关键．
练习册系列答案
相关题目
己知：四点A、B、C、D的位置如图所示，根据下列语句，画出图形．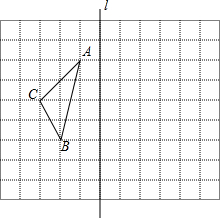
如图所示的方格纸中，每一个小正方形的边长都是1，网格中有一个格点三角形ABC．