题目内容
19. 在如图的网格图中,每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=4.
在如图的网格图中,每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=4.(1)试在图中做出△ABC以A为旋转中心,沿顺时针方向旋转90°后的图形△AB1C1;
(2)若点B的坐标为(-3,5),试在图中画出平面直角坐标系,并标出A、C两点的坐标;
(3)根据(2)的坐标系,以B为位似中心,做△BA2C2,使△BA2C2与△ABC位似,且△BA2C2与△ABC位似比为2:1,并直接写出A2的坐标.
分析 (1)直接利用旋转的性质得出对应点位置进而得出答案;
(2)利用B点坐标得出原点位置,进而得出A、C两点的坐标;
(3)利用位似图形的性质得出对应点位置,进而得出答案.
解答  解:(1)如图所示:△AB1C1,即为所求;
解:(1)如图所示:△AB1C1,即为所求;
(2)如图所示:A(0、1)、C(-3、1);
(3)如图所示:△BA2C2,即为所求,A2(3、-3 ).
点评 此题主要考查了位似变换以及旋转变换,正确得出对应点位置是解题关键.

练习册系列答案
相关题目
 已知:如图,点E,C在线段BF上,AC=DF,AC∥DF,BE=CF.求证:AB∥DE.
已知:如图,点E,C在线段BF上,AC=DF,AC∥DF,BE=CF.求证:AB∥DE.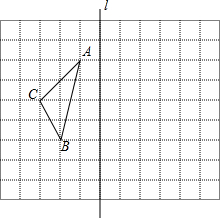 如图所示的方格纸中,每一个小正方形的边长都是1,网格中有一个格点三角形ABC.
如图所示的方格纸中,每一个小正方形的边长都是1,网格中有一个格点三角形ABC. 如图,一副三角板的两个直角顶点重合在一起.
如图,一副三角板的两个直角顶点重合在一起.
 小明参加某网店的“翻牌抽奖”活动,如图,4张牌分别对应价值5,10,15,20(单位:元)的4件奖品.
小明参加某网店的“翻牌抽奖”活动,如图,4张牌分别对应价值5,10,15,20(单位:元)的4件奖品.