题目内容
13.开学初,小芳和小亮取学校商店购买学习用品,小芳用18元买了1支水笔和3本笔记本,小亮用了26元买了同样的2支水笔和4本笔记本.(1)求每支水笔和每本笔记本的价格;
(2)校运动会后,班主任拿出100元班费交给体育委员,购买上述价格的水笔和笔记本共24件作为奖品,奖给校运动会上表现突出的同学,要求笔记本的数量不少于水笔的数量,问共有多少种购买方案?请你一一列举出来.
分析 (1)根据1支水笔的价钱+3本笔记本的价钱=18,2支水笔的价钱+4本笔记本的价钱=26这两个等量关系列出方程组,求解即可;
(2)设水笔a支,笔记本(24-a)本,根据水笔和笔记本共24件作为奖品,笔记本的数量不少于水笔的数量,列出不等式组,再进行求解即可得出答案.
解答 解:(1)设每支水笔x元,每本笔记本y元,
则根据题意,得$\left\{\begin{array}{l}{x+3y=18}\\{2x+4y=26}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=3}\\{y=5}\end{array}\right.$,
答:每支水笔3元,每本笔记本5元.
(2)设水笔a支,笔记本(24-a)本,
则根据题意,得$\left\{\begin{array}{l}{3a+5(24-a)≤100}\\{24-a≥a}\end{array}\right.$,
解得10≤a≤12.
∵a为正整数,
∴a=10,11,12.
∴共有3种购买方案,分别是:
方案1:购买水笔10支,笔记本14本.
方案2:购买水笔11支,笔记本13本.
方案3:购买水笔12支,笔记本12本.
点评 本题考查了一元一次不等式组的应用和二元一次方程组的应用,将现实生活中的事件与数学思想联系起来,读懂题列出不等式组和二元一次方程组,即可求解.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
3.下列图形中,是中心对称图形但不是轴对称的图形是( )
| A. |  等边三角形 | B. |  正方形 | C. |  圆 | D. |  平行四边形 平行四边形 |
8.点A在第二象限,距离x轴3个单位长度,距离y轴4个单位长度,则点A的坐标是( )
| A. | (-3,4) | B. | (3,-4) | C. | (-4,3) | D. | (4,-3) |
18.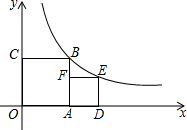 如若正方形OABC的顶点B和正方形ADEF的顶点E都在反比例函数y=$\frac{1}{x}$(x>0)的图象上,则E点的坐标是( )
如若正方形OABC的顶点B和正方形ADEF的顶点E都在反比例函数y=$\frac{1}{x}$(x>0)的图象上,则E点的坐标是( )
 如若正方形OABC的顶点B和正方形ADEF的顶点E都在反比例函数y=$\frac{1}{x}$(x>0)的图象上,则E点的坐标是( )
如若正方形OABC的顶点B和正方形ADEF的顶点E都在反比例函数y=$\frac{1}{x}$(x>0)的图象上,则E点的坐标是( )| A. | $({\frac{{\sqrt{5}-1}}{2},\frac{{\sqrt{5}+1}}{2}})$ | B. | $({\frac{{\sqrt{5}+1}}{2},\frac{{\sqrt{5}-1}}{2}})$ | C. | $({\frac{{\sqrt{5}}}{2},-\frac{{\sqrt{5}}}{2}})$ | D. | (1,1) |
3. 如图,在△ABC中,∠BAC=50°,将△ABC绕点A逆时针旋转80°得到△AB′C,则∠CAB′的度数为( )
如图,在△ABC中,∠BAC=50°,将△ABC绕点A逆时针旋转80°得到△AB′C,则∠CAB′的度数为( )
 如图,在△ABC中,∠BAC=50°,将△ABC绕点A逆时针旋转80°得到△AB′C,则∠CAB′的度数为( )
如图,在△ABC中,∠BAC=50°,将△ABC绕点A逆时针旋转80°得到△AB′C,则∠CAB′的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 80° |
 某学校期末考试要给学生印制复习资料若干份,印刷厂有甲、乙两种收费方式,除按印刷份数收取印刷费用外,甲种方式还收取制版费,而乙种不需要,两种印刷方式的费用y(元)与印刷份数x(份)之间的函数关系如图所示:
某学校期末考试要给学生印制复习资料若干份,印刷厂有甲、乙两种收费方式,除按印刷份数收取印刷费用外,甲种方式还收取制版费,而乙种不需要,两种印刷方式的费用y(元)与印刷份数x(份)之间的函数关系如图所示: 如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8,…,顶点依次为A1,A2,A3,A4,…表示,则顶点A2018的坐标是(-505,505).
如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8,…,顶点依次为A1,A2,A3,A4,…表示,则顶点A2018的坐标是(-505,505).