题目内容
3．解不等式组$\left\{\begin{array}{l}{2x-2＜3x①}\\{\frac{x+2}{5}-\frac{x-1}{4}≥\frac{1}{2}②}\end{array}\right.$，并在数轴上把它的解集表示出来．分析 分别求出每一个不等式的解集，再根据“大于向右，小于向左，包括端点用实心，不包括端点用空心”的原则在数轴上将解集表示出来，即可得不等式组的解集．
解答 解：解不等式①，得：x＞-2，
解不等式②，得：x≤3，
如图，在同一数轴上表示不等式①、②的解集：
可知不等式组的解集是：-2＜x≤3．
点评 本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，将矩形ABCD沿对角线AC折叠，点B落在点E处，请用尺规作出点E．（不写画法，保留作图痕迹）
如图，在正方形ABCD中，E、F是对角线BD上两点，且∠EAF=45°，将△ADF绕点A顺时针旋转90°后，得到△ABQ，连接EQ，求证：
18．
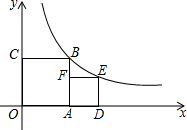如若正方形OABC的顶点B和正方形ADEF的顶点E都在反比例函数y=$\frac{1}{x}$（x＞0）的图象上，则E点的坐标是（ ）
如若正方形OABC的顶点B和正方形ADEF的顶点E都在反比例函数y=$\frac{1}{x}$（x＞0）的图象上，则E点的坐标是（ ）| A． | $（{\frac{{\sqrt{5}-1}}{2}，\frac{{\sqrt{5}+1}}{2}}）$ | B． | $（{\frac{{\sqrt{5}+1}}{2}，\frac{{\sqrt{5}-1}}{2}}）$ | C． | $（{\frac{{\sqrt{5}}}{2}，-\frac{{\sqrt{5}}}{2}}）$ | D． | （1，1） |
已知一次函数y=kx+b经过（-1，2），且与y轴交点的纵坐标为4，求一次函数的解析式并画出此函数的图象．
12．
如图，点O是矩形ABCD的中心，E是AB上的点，沿CE折叠后，点B恰好与点O重合，若BC=3，则折痕CE的长为（ ）
如图，点O是矩形ABCD的中心，E是AB上的点，沿CE折叠后，点B恰好与点O重合，若BC=3，则折痕CE的长为（ ）| A． | 2$\sqrt{3}$ | B． | $\frac{3\sqrt{3}}{2}$ | C． | $\sqrt{3}$ | D． | 6 |
13．正比例函数y=-2x的大致图象是（ ）
| A． |  | B． |  | C． |  | D． |  |