题目内容
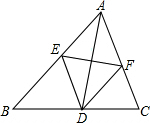 如图,在△ABC中,AD是角平分线,AD的垂直平分线分别交AB,AC于点E,F.试判断定四边形AEDF的形状,并证明你的结论.
如图,在△ABC中,AD是角平分线,AD的垂直平分线分别交AB,AC于点E,F.试判断定四边形AEDF的形状,并证明你的结论.考点:菱形的判定,线段垂直平分线的性质
专题:
分析:由EF垂直平分AD,根据线段垂直平分线的性质可得AE=DE,AF=DF,又由AD平分∠BAC,易证得△ADE≌△AFD,则可得AE=AF,即可得AE=DE=DF=AF,则可判定四边形AEDF是菱形.
解答:解:四边形AEDF是菱形.
理由:∵EF垂直平分AD,
∴AE=DE,AF=DF,
∴∠EAD=∠EDA,∠FAD=∠FDA,
∵AD平分∠BAC,
∴∠EAD=∠FAD,
∴∠ADE=∠ADF,
在△ADE和△AFD中,
,
∴△ADE≌△AFD(ASA),
∴AE=AF,
∴AE=DE=DF=AF,
∴四边形AEDF是菱形.
理由:∵EF垂直平分AD,
∴AE=DE,AF=DF,
∴∠EAD=∠EDA,∠FAD=∠FDA,
∵AD平分∠BAC,
∴∠EAD=∠FAD,
∴∠ADE=∠ADF,
在△ADE和△AFD中,
|
∴△ADE≌△AFD(ASA),
∴AE=AF,
∴AE=DE=DF=AF,
∴四边形AEDF是菱形.
点评:此题考查了菱形的判定、线段垂直平分线的性质以及全等三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
 如图,OC是∠AOB的平分线,∠AOB=61°30′,求与∠AOC互补的角的大小.
如图,OC是∠AOB的平分线,∠AOB=61°30′,求与∠AOC互补的角的大小.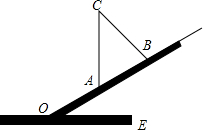 如图,一个坡度为1:
如图,一个坡度为1: 已知AB∥DE,∠B=∠E,说明BC∥EF.
已知AB∥DE,∠B=∠E,说明BC∥EF.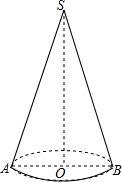 如图,过圆锥的顶点S和底面圆的圆心O的平面截圆锥得截面△SAB,其中SA=SB,AB是圆锥底面圆O的直径,已知SA=7cm,AB=4cm,求截面△SAB的面积.
如图,过圆锥的顶点S和底面圆的圆心O的平面截圆锥得截面△SAB,其中SA=SB,AB是圆锥底面圆O的直径,已知SA=7cm,AB=4cm,求截面△SAB的面积. 已知:如图,?ABCD中,M为BC中点,∠MBC=∠MCB.求证:四边形ABCD是矩形.
已知:如图,?ABCD中,M为BC中点,∠MBC=∠MCB.求证:四边形ABCD是矩形.