题目内容
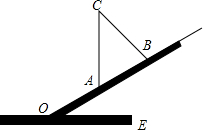 如图,一个坡度为1:
如图,一个坡度为1:| 3 |
| 3 |
| 2 |
考点:解直角三角形的应用-坡度坡角问题
专题:
分析:延长CA交CE于点D,过点B作BH⊥AC于点F,根据坡度角的应用求出∠BOD=30°得出∠BAF=60°,再根据勾股定理得出求出BF,从而求出BC和AC的值,最后根据AC+BC是大树在折断前的高,即可得出答案.
解答: 解:延长CA交CE于点D,过点B作BH⊥AC于点F,
解:延长CA交CE于点D,过点B作BH⊥AC于点F,
∵坡度为1:
,
∴∠BOD=30°,
∴∠OAD=60°,
∴∠BAF=60°,
∵AB=4,
∴AF=2,
∴BF=
=2
,
∵∠BCA=45°,
∴CF=BF=2
,
∴BC=
=2
,AC=2+2
,
∴AC+BC=2+2
+2
=2+2×1.73+2×1.73×1.41≈10.34(米),
答:大树在折断前高10.34米.
 解:延长CA交CE于点D,过点B作BH⊥AC于点F,
解:延长CA交CE于点D,过点B作BH⊥AC于点F,∵坡度为1:
| 3 |
∴∠BOD=30°,
∴∠OAD=60°,
∴∠BAF=60°,
∵AB=4,
∴AF=2,
∴BF=
| 42-22 |
| 3 |
∵∠BCA=45°,
∴CF=BF=2
| 3 |
∴BC=
(2
|
| 6 |
| 3 |
∴AC+BC=2+2
| 3 |
| 6 |
答:大树在折断前高10.34米.
点评:本题考查了解直角三角形的应用,用到的知识点是直角三角形的性质、勾股定理的运用,解题的关键是根据题意作出辅助线,构造直角三角形.

练习册系列答案
相关题目
根式①
;②
;③
中,化成最简二次根式后与
的被开方式相同的二次根式的是( )
| 12 |
| 24 |
|
| 6 |
| A、只有② | B、有①③ |
| C、有②③ | D、不存在 |
 有一水库大坝的横截面是梯形ABCD,AD∥BC,EF为水库的水面,点E在DC上,某课题小组在老师的带领下想测量水的深度,他们测得背水坡AB的长为12米,迎水坡上DE的长为2米,∠BAD=135°,∠ADC=120°.
有一水库大坝的横截面是梯形ABCD,AD∥BC,EF为水库的水面,点E在DC上,某课题小组在老师的带领下想测量水的深度,他们测得背水坡AB的长为12米,迎水坡上DE的长为2米,∠BAD=135°,∠ADC=120°. 甲与乙两个城市间计划修建一条城际铁路,其中有一段路基的横段面设计上底宽4
甲与乙两个城市间计划修建一条城际铁路,其中有一段路基的横段面设计上底宽4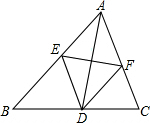 如图,在△ABC中,AD是角平分线,AD的垂直平分线分别交AB,AC于点E,F.试判断定四边形AEDF的形状,并证明你的结论.
如图,在△ABC中,AD是角平分线,AD的垂直平分线分别交AB,AC于点E,F.试判断定四边形AEDF的形状,并证明你的结论. 如图,在Rt△ABC中,∠C=90°,∠A=30°,AC=
如图,在Rt△ABC中,∠C=90°,∠A=30°,AC=