题目内容
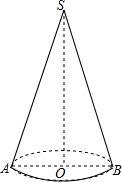 如图,过圆锥的顶点S和底面圆的圆心O的平面截圆锥得截面△SAB,其中SA=SB,AB是圆锥底面圆O的直径,已知SA=7cm,AB=4cm,求截面△SAB的面积.
如图,过圆锥的顶点S和底面圆的圆心O的平面截圆锥得截面△SAB,其中SA=SB,AB是圆锥底面圆O的直径,已知SA=7cm,AB=4cm,求截面△SAB的面积.考点:圆锥的计算
专题:计算题
分析:先利用勾股定理计算出SO,然后根据三角形面积公式求解.
解答:解:在Rt△AOS中,∵OA=
AB=2,SA=7,
∴SO=
=3
,
∴截面△SAB的面积=
×4×3
=6
(cm2).
| 1 |
| 2 |
∴SO=
| SA2-AO2 |
| 5 |
∴截面△SAB的面积=
| 1 |
| 2 |
| 5 |
| 5 |
点评:本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.

练习册系列答案
相关题目
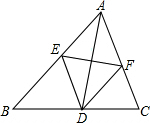 如图,在△ABC中,AD是角平分线,AD的垂直平分线分别交AB,AC于点E,F.试判断定四边形AEDF的形状,并证明你的结论.
如图,在△ABC中,AD是角平分线,AD的垂直平分线分别交AB,AC于点E,F.试判断定四边形AEDF的形状,并证明你的结论. 已知:如图AC、BD的交点O是四边形ABCD的对称中心,且∠A=90°.求证:四边形ABCD是矩形.
已知:如图AC、BD的交点O是四边形ABCD的对称中心,且∠A=90°.求证:四边形ABCD是矩形.