题目内容
计算:(a-b)2n+1(b-a)2n-1÷(a-b)4n.
考点:同底数幂的除法,同底数幂的乘法,幂的乘方与积的乘方
专题:
分析:根据负数的奇数次幂是负数,可化成同底数幂的乘除法,根据同底数幂的乘除法,可得答案.
解答:解:原式=(a-b)2n+1[-(a-b)2n-1]÷(a-b)4n
=-(a-b)2n+1+2n-1-4n
=-(a-b)0
=1.
=-(a-b)2n+1+2n-1-4n
=-(a-b)0
=1.
点评:本题考查了同底数幂的除法,先利用负数的奇数次幂是负数化成同底数幂的乘除法,再利用同底数幂的乘除法.

练习册系列答案
相关题目
 甲与乙两个城市间计划修建一条城际铁路,其中有一段路基的横段面设计上底宽4
甲与乙两个城市间计划修建一条城际铁路,其中有一段路基的横段面设计上底宽4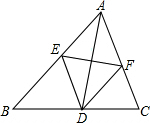 如图,在△ABC中,AD是角平分线,AD的垂直平分线分别交AB,AC于点E,F.试判断定四边形AEDF的形状,并证明你的结论.
如图,在△ABC中,AD是角平分线,AD的垂直平分线分别交AB,AC于点E,F.试判断定四边形AEDF的形状,并证明你的结论. 蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米(小方格的边长为1厘米)
蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米(小方格的边长为1厘米) 如图,在Rt△ABC中,∠C=90°,∠A=30°,AC=
如图,在Rt△ABC中,∠C=90°,∠A=30°,AC= 如图所示,长方形中有两个正方形,已知大正方形的面积为75cm2,小正方形的面积为27cm2,求阴影部分的面积.
如图所示,长方形中有两个正方形,已知大正方形的面积为75cm2,小正方形的面积为27cm2,求阴影部分的面积.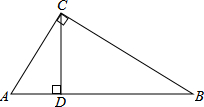 如图,在Rt△ABC中,∠C=90°,BC=15,AB-AC=9,CD⊥AB于点D,求CD的长.
如图,在Rt△ABC中,∠C=90°,BC=15,AB-AC=9,CD⊥AB于点D,求CD的长.