题目内容
14.已知在△ABC中,AD是BC边上的高,AD=2,BD=2,CD=2$\sqrt{3}$,求∠BAC的度数.分析 先由AD是BC边上的高得出AD⊥BC于D,再解直角△ABD得出∠BAD=45°,解直角△ACD,得出∠CAD=60°,然后分AD在△ABC内部与AD在△ABC外部两种情况分别求出∠BAC的度数.
解答  解:如图.
解:如图.
∵AD是BC边上的高,
∴AD⊥BC于D.
在直角△ABD中,∵∠ADB=90°,AD=2,BD=2,
∴∠BAD=45°.
在直角△ACD中,∵∠ADB=90°,AD=2,CD=2$\sqrt{3}$,
∴tan∠CAD=$\frac{CD}{AD}$=$\frac{2\sqrt{3}}{2}$=$\sqrt{3}$,
∴∠CAD=60°.
当AD在△ABC内部时,∠BAC=∠CAD+∠BAD=60°+45°=105°;
当AD在△ABC外部时,∠BAC=∠CAD-∠BAD=60°-45°=15°.
故∠BAC的度数为105°或15°.
点评 本题考查了解直角三角形,三角形的高,利用数形结合与分类讨论是解题的关键.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
4.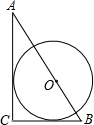 如图,Rt△ABC中,∠C=90°,O是AB边上一点,⊙O与AC、BC都相切.若BC=6,AC=8,则⊙O的半径为( )
如图,Rt△ABC中,∠C=90°,O是AB边上一点,⊙O与AC、BC都相切.若BC=6,AC=8,则⊙O的半径为( )
 如图,Rt△ABC中,∠C=90°,O是AB边上一点,⊙O与AC、BC都相切.若BC=6,AC=8,则⊙O的半径为( )
如图,Rt△ABC中,∠C=90°,O是AB边上一点,⊙O与AC、BC都相切.若BC=6,AC=8,则⊙O的半径为( )| A. | $\frac{24}{7}$ | B. | 4 | C. | 5 | D. | 2 |
19.若⊙O的半径为5,OP=5,则点P与⊙O的位置关系是( )
| A. | 点P在⊙O内 | B. | 点P在⊙O上 | C. | 点P在⊙O外 | D. | 点P在⊙O上或⊙O外 |
 如图,AC∥BD,AD、BC相交于E,EF∥BD,求证:$\frac{1}{AC}$+$\frac{1}{BD}$=$\frac{1}{EF}$.
如图,AC∥BD,AD、BC相交于E,EF∥BD,求证:$\frac{1}{AC}$+$\frac{1}{BD}$=$\frac{1}{EF}$.