题目内容
7.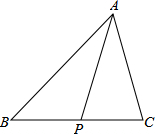 如图,在△ABC中,记$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,点P为BC的中点,则$\overrightarrow{AP}$=$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$(用向量$\overrightarrow{a}$、$\overrightarrow{b}$来表示)
如图,在△ABC中,记$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,点P为BC的中点,则$\overrightarrow{AP}$=$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$(用向量$\overrightarrow{a}$、$\overrightarrow{b}$来表示)
分析 由三角形法则可求得$\overrightarrow{BC}$的长,又由点P为BC的中点,即可求得$\overrightarrow{BP}$,再利用三角形法则求解即可求得答案.
解答 解:∵$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,
∴$\overrightarrow{BC}$=$\overrightarrow{AC}$-$\overrightarrow{AB}$=$\overrightarrow{b}$-$\overrightarrow{a}$,
∵点P为BC的中点,
∴$\overrightarrow{BP}$=$\frac{1}{2}$$\overrightarrow{BC}$=$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$,
∴$\overrightarrow{AP}$=$\overrightarrow{AB}$+$\overrightarrow{BP}$=$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$=$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$.
故答案为:$\frac{1}{2}\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}$.
点评 此题考查了平面向量的知识.注意掌握三角形法则的应用是解此题的关键.

 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案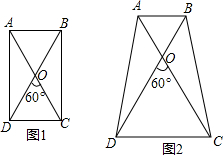 已知:在四边形ABCD中,AC=BD,AC与BD交于点O,∠DOC=60度.
已知:在四边形ABCD中,AC=BD,AC与BD交于点O,∠DOC=60度.
 (针孔成像问题)根据图中尺寸(AB∥A′B′),那么物像长y(A′B′的长)与x的函数图象是( )
(针孔成像问题)根据图中尺寸(AB∥A′B′),那么物像长y(A′B′的长)与x的函数图象是( )



 如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合的部分构成了一个四边形
如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合的部分构成了一个四边形 如图,已知直线y=4-x与反比例函数y=$\frac{m}{x}$(m>0,x>0)的图象交于A,B两点,与x轴,y轴分别相交于C,D两点.
如图,已知直线y=4-x与反比例函数y=$\frac{m}{x}$(m>0,x>0)的图象交于A,B两点,与x轴,y轴分别相交于C,D两点.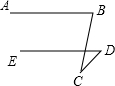 如图所示,AB∥DE,如果点C在AB与ED之外,其他条件不变,那么∠ABC、∠CDE与∠BCD之间会有怎样的数量关系,请证明,你还能就本题作出什么新的猜想?
如图所示,AB∥DE,如果点C在AB与ED之外,其他条件不变,那么∠ABC、∠CDE与∠BCD之间会有怎样的数量关系,请证明,你还能就本题作出什么新的猜想?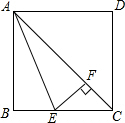 如图所示,正方形ABCD的边长为1,AC是对角线,AE平分∠BAC,EF⊥AC于点F.
如图所示,正方形ABCD的边长为1,AC是对角线,AE平分∠BAC,EF⊥AC于点F.