题目内容
2.当x满足-3≤x≤-2时,不等式$\frac{3{x}^{2}+4x-a}{x+1}$>3x-1恒成立,则a的取值范围为( )| A. | a>-3 | B. | a>-5 | C. | a<-3 | D. | a<-5 |
分析 先根据x的取值范围确定出x+1的符号,再由不等式恒成立用a表示出x的取值范围,进而可得出结论.
解答 解:∵x满足-3≤x≤-2,
∴x+1<0.
∵不等式$\frac{3{x}^{2}+4x-a}{x+1}$>3x-1恒成立,
∴3x2+4x-a<(x+1)(3x-1),
∴x<$\frac{a-1}{2}$.
∵-3≤x≤-2,
∴$\frac{a-1}{2}$>-2,
∴a>-3.
故选A.
点评 本题考查的是不等式的性质,熟知不等式的两边同时乘以(或除以)同一个负数,不等号的方向改变是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.在平面直角坐标系中,点P(-2,a)与点Q(b,3)关于原点对称,则a+b的值为( )
| A. | 5 | B. | -5 | C. | 1 | D. | -1 |
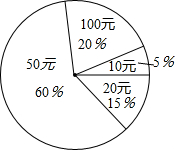 在雅安地震救灾捐款活动中,某校6000名同学每人都捐了款,有捐10元的,有捐20元的,还有捐50元、100元的,如图统计图反映了不同捐款的人数和比例,那么该校同学平均每人捐款53.5元.
在雅安地震救灾捐款活动中,某校6000名同学每人都捐了款,有捐10元的,有捐20元的,还有捐50元、100元的,如图统计图反映了不同捐款的人数和比例,那么该校同学平均每人捐款53.5元. 如图,在边长为1的正方形中,被4段$\frac{1}{4}$圆弧所围的阴影部分面积为1-$\sqrt{3}$+$\frac{π}{3}$.
如图,在边长为1的正方形中,被4段$\frac{1}{4}$圆弧所围的阴影部分面积为1-$\sqrt{3}$+$\frac{π}{3}$.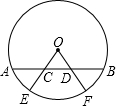 已知:如图,AB是⊙O的弦,且AC=BD,半径OE,OF分别过C,D两点,求证:$\widehat{AE}$=$\widehat{BF}$.
已知:如图,AB是⊙O的弦,且AC=BD,半径OE,OF分别过C,D两点,求证:$\widehat{AE}$=$\widehat{BF}$.