Question

12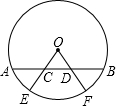．已知：如图，AB是⊙O的弦，且AC=BD，半径OE，OF分别过C，D两点，求证：$\widehat{AE}$=$\widehat{BF}$．

Answer 1

分析 由等腰三角形的性质得出∠A=∠B，由SAS证明△OAC≌△OBD，得出∠AOC=∠BOD，即可得出结论．

解答 证明：连接OA、OB，如图所示：
∵OA=OB，
∴∠A=∠B，
在△OAC和△OBD中，$\left\{\begin{array}{l}{OA=OB}&{\;}\\{∠A=∠B}&{\;}\\{AC=BD}&{\;}\end{array}\right.$，
∴△OAC≌△OBD（SAS），
∴∠AOC=∠BOD，
∴$\widehat{AE}$=$\widehat{BF}$．

点评 本题考查了圆心角、弧、弦的关系，全等三角形的判定与性质，等腰三角形的性质；熟练掌握圆心角、弧、弦的关系，证明三角形全等是解决问题的关键．