题目内容
3.在平面直角坐标系中,O为坐标原点,点B在x轴正半轴上,点D在y轴正半轴上,OB=OD=3,C是第一象限内的点,且△BOD和△BCD关于直线BD轴对称.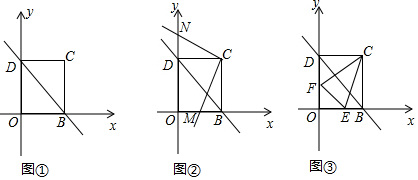
(1)如图①,则点C的坐标为(3,3).
(2)如图②,点M(m,0),N(0,n)(3<n<6),若∠MCN=90°,求m+n的值;
(3)如图③,若E、F分别为线段OB与线段OD上的动点(不包含线段端点),且∠ECF=45°,那么△OEF的周长是否是个定值?如果是,请求出这个定值;如果不是,请说明理由.
分析 (1)根据折叠的性质证明矩形OBCD是正方形,得到答案;
(2)证明△DCN≌△BCM,根据全等三角形的性质解答;
(3)以点C为旋转中心把△CDF逆时针旋转90°,得到△CBH,证明△FCE≌△HCE,求出△OEF的周长是定值.
解答 解:(1)∵OB=OD,
∴∠ODB=∠OBD=45°,
由折叠的性质可知,∠OBC=2∠OBD=90°,∠ODC=2∠ODB=90°,
又∠DOB=90°,
∴四边形OBCD是矩形,又OB=OD,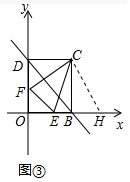
∴矩形OBCD是正方形,
∴点C的坐标为(3,3)
故答案为3;3;
(2)∵∠MCN=90°,∠DCB=90°,
∴∠DCN=∠BCM,
在△DCN和△BCM中,
$\left\{\begin{array}{l}{∠DCM=∠BCN}\\{CD=CB}\\{∠CDN=∠CBM}\end{array}\right.$,
∴△DCN≌△BCM,
∴DN=BM,
∴m+n=OB-BN+OD+DN=OB+OD=6;
(3)△OEF的周长是定值6,
以点C为旋转中心把△CDF逆时针旋转90°,得到△CBH,
∵∠ECF=45°,∠DCB=90°,
∴∠DCF+∠ECB=45°,
∴∠ECH=45°,
在△FCE和△HCE中,
$\left\{\begin{array}{l}{∠CF=CH}\\{∠FCE=∠HCE}\\{CE=CE}\end{array}\right.$,
∴△FCE≌△HCE,
∴EF=EH,
∴△OEF的周长=OF+OE+EF=OF+OE+BE+DF=3+3=6.
点评 本题考查的是全等三角形的判定和性质、轴对称的性质,掌握全等三角形的判定定理和性质定理是解题的关键.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
14.下列计划图形,不一定是轴对称图形的是( )
| A. | 角 | B. | 等腰三角形 | C. | 长方形 | D. | 直角三角形 |
11.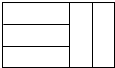 五个完全相同的小长方形拼成如图所示的大长方形,大长方形的周长是32cm,则小长方形的面积是( )
五个完全相同的小长方形拼成如图所示的大长方形,大长方形的周长是32cm,则小长方形的面积是( )
 五个完全相同的小长方形拼成如图所示的大长方形,大长方形的周长是32cm,则小长方形的面积是( )
五个完全相同的小长方形拼成如图所示的大长方形,大长方形的周长是32cm,则小长方形的面积是( )| A. | 8cm2 | B. | 10cm2 | C. | 12cm2 | D. | 16cm2 |
18.设点M(x,y)在第二象限,且|x|=2,|y|=3,则点M关于y轴的对称点的坐标是( )
| A. | (2,3) | B. | (-2,3) | C. | (-3,2) | D. | (-3,-2) |
8.多项式4x2+□+1是一个完全平方式,那么“□”可以是( )
| A. | 2x | B. | -2x | C. | 4x | D. | -4x4 |
 在如图所示的正方形网格中,每个小正方形的边长均为1,格点三角形ABC(顶点是网格线交点的三角形)的顶点A、C的坐标分别为(-4,5)、(-1,3)
在如图所示的正方形网格中,每个小正方形的边长均为1,格点三角形ABC(顶点是网格线交点的三角形)的顶点A、C的坐标分别为(-4,5)、(-1,3)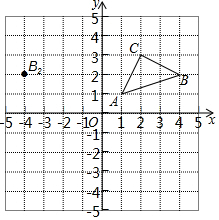 如图所示,在直角坐标系xOy中,△ABC三点的坐标分别为A(1,1),B(4,2),C(2,3).
如图所示,在直角坐标系xOy中,△ABC三点的坐标分别为A(1,1),B(4,2),C(2,3).