题目内容
4.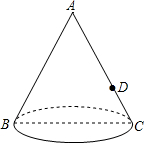 如图,圆锥的轴截面(过圆锥顶点和底面圆心的截面)是边长为2cm的等边△ABC,点D是AC的中点,一只蚂蚁从点B出发沿圆锥的表面爬行到点D处,则这只蚂蚁爬行的最短距离是$\sqrt{5}$cm.
如图,圆锥的轴截面(过圆锥顶点和底面圆心的截面)是边长为2cm的等边△ABC,点D是AC的中点,一只蚂蚁从点B出发沿圆锥的表面爬行到点D处,则这只蚂蚁爬行的最短距离是$\sqrt{5}$cm.
分析 根据圆锥的轴截面是边长为4cm的等边三角形可知,展开图是半径是4的半圆.点B是半圆的一个端点,而点D是平分半圆的半径的中点,根据勾股定理就可求出两点B和D在展开图中的距离,就是这只蚂蚁爬行的最短距离.
解答 解:∵圆锥的底面周长是2π,则2π=$\frac{nπ•2}{180}$,
∴n=180°即圆锥侧面展开图的圆心角是180°,
∴在圆锥侧面展开图中AD=1,AB=2,∠BAD=90°,
∴在圆锥侧面展开图中BD=$\sqrt{5}$,
∴这只蚂蚁爬行的最短距离是$\sqrt{5}$cm.
故答案为:$\sqrt{5}$.
点评 本题考查了平面展开--最短路径问题,正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
14.把拋物线y=(x-1)2+2向右平移1个单位,再向下平移3个单位,所得抛物线是( )
| A. | y=x2+5 | B. | y=(x-2)2-l | C. | y=(x-2)2-3 | D. | y=x2-1 |
13.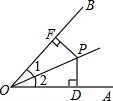 如图,∠1=∠2,PD⊥OA于D,PF⊥OB于F,下列结论错误的是( )
如图,∠1=∠2,PD⊥OA于D,PF⊥OB于F,下列结论错误的是( )
 如图,∠1=∠2,PD⊥OA于D,PF⊥OB于F,下列结论错误的是( )
如图,∠1=∠2,PD⊥OA于D,PF⊥OB于F,下列结论错误的是( )| A. | PD=PF | B. | OD=OF | C. | ∠DPO=∠FPO | D. | PD=OD |
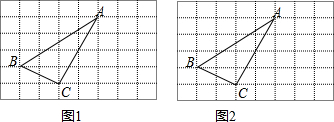
 如图,华庆号船位于航海图上平面直角坐标系中的点A(10,2)处时,点C、海岛B的位置在y轴上,且∠CBA=30°,∠CAB=60°.若海岛B周围16海里内有海礁,华庆号船继续沿AC向C航行有无触礁危险?请说明理由.
如图,华庆号船位于航海图上平面直角坐标系中的点A(10,2)处时,点C、海岛B的位置在y轴上,且∠CBA=30°,∠CAB=60°.若海岛B周围16海里内有海礁,华庆号船继续沿AC向C航行有无触礁危险?请说明理由.