题目内容
13.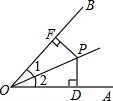 如图,∠1=∠2,PD⊥OA于D,PF⊥OB于F,下列结论错误的是( )
如图,∠1=∠2,PD⊥OA于D,PF⊥OB于F,下列结论错误的是( )| A. | PD=PF | B. | OD=OF | C. | ∠DPO=∠FPO | D. | PD=OD |
分析 根据角平分线性质得出PF=PD,根据勾股定理推出OF=OD,根据三角形内角和定理推出∠DPO=∠FPO.
解答 解:A、∵∠1=∠2,PD⊥OA,PF⊥OB,
∴PE=PD,正确,故本选项错误;
B、∵PD⊥OA,PF⊥OB,
∴∠PFO=∠PDO=90°,
∵OP=OP,PF=PD,
∴由勾股定理得:OF=OD,正确,故本选项错误;
C、∵∠PFO=∠PDO=90°,∠POB=∠POA,
∴由三角形的内角和定理得:∠DPO=∠FPO,正确,故本选项错误;
D、根据已知不能推出PD=OD,错误,故本选项正确;
故选D.
点评 本题主要考查平分线的性质,三角形的内角和,熟练掌握角平分线的性质是解题的关键.

练习册系列答案
相关题目
3.下列各式计算正确的是( )
| A. | a2•a3=a6 | B. | (2a2b3)3=6a6b6 | C. | (a3)4=a12 | D. | 2a+3b=5ab |
1.正六边形的内角和为( )
| A. | 180° | B. | 360° | C. | 540° | D. | 720° |
18.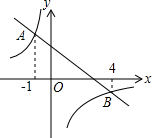 已知如图,一次函数y=ax+b和反比例函数y=$\frac{k}{x}$的图象相交于A、B两点,使不等式ax+b>$\frac{k}{x}$成立的自变量x的取值范围是( )
已知如图,一次函数y=ax+b和反比例函数y=$\frac{k}{x}$的图象相交于A、B两点,使不等式ax+b>$\frac{k}{x}$成立的自变量x的取值范围是( )
 已知如图,一次函数y=ax+b和反比例函数y=$\frac{k}{x}$的图象相交于A、B两点,使不等式ax+b>$\frac{k}{x}$成立的自变量x的取值范围是( )
已知如图,一次函数y=ax+b和反比例函数y=$\frac{k}{x}$的图象相交于A、B两点,使不等式ax+b>$\frac{k}{x}$成立的自变量x的取值范围是( )| A. | x<-1或x>4 | B. | -1<x<4 | C. | x<-1或0<x<4 | D. | -1<x<0或x>4 |
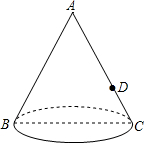 如图,圆锥的轴截面(过圆锥顶点和底面圆心的截面)是边长为2cm的等边△ABC,点D是AC的中点,一只蚂蚁从点B出发沿圆锥的表面爬行到点D处,则这只蚂蚁爬行的最短距离是$\sqrt{5}$cm.
如图,圆锥的轴截面(过圆锥顶点和底面圆心的截面)是边长为2cm的等边△ABC,点D是AC的中点,一只蚂蚁从点B出发沿圆锥的表面爬行到点D处,则这只蚂蚁爬行的最短距离是$\sqrt{5}$cm.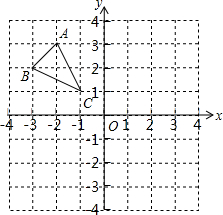 如图,在坐标系xOy中,A(-2,3),B(-3,2),C(-1,1),
如图,在坐标系xOy中,A(-2,3),B(-3,2),C(-1,1),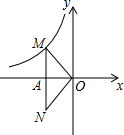 已知反比例函数y=$\frac{m-5}{x}$的图象的一支位于第二象限.
已知反比例函数y=$\frac{m-5}{x}$的图象的一支位于第二象限.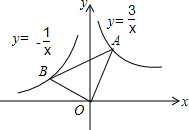 如图,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转,若∠BOA的两边分别与函数y=-$\frac{1}{x}$,y=$\frac{3}{x}$的图象交于B、A两点,则∠OAB的大小的变化趋势为( )
如图,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转,若∠BOA的两边分别与函数y=-$\frac{1}{x}$,y=$\frac{3}{x}$的图象交于B、A两点,则∠OAB的大小的变化趋势为( )