题目内容
19.正六边形的边长为2,它的外接圆与内切圆所组成的圆环的面积为π.分析 由正六边形的性质得出正六边形的半径=边长=2,由三角函数求出内切圆半径,即可求出它的外接圆与内切圆所组成的圆环的面积.
解答  解:设AB为正六边形的边长,O为正六边形的中心,OC为正六边形的边心距,即为正六边形的内切圆半径,如图所示:
解:设AB为正六边形的边长,O为正六边形的中心,OC为正六边形的边心距,即为正六边形的内切圆半径,如图所示:
∵正六边形的边长为2,
则它的外接圆的半径OA=AB=2,
它的内切圆的半径OC=OA•sin60°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
所以圆环的面积=π[22-($\sqrt{3}$)2]=π;
故答案为:π.
点评 本题考查了正六边形的性质、正六边形的边长与它的外接圆的半径的关系,内切圆的半径的计算及圆的面积公式、三角函数等知识;由正六边形的性质和三角函数求出外接圆与内切圆半径是解题的关键.

练习册系列答案
相关题目
7.下列说法中不正确的是( )
| A. | 想了解某种饮料中含色素的情况,宜抽样调查 | |
| B. | 数据1,1,2,2,3的中位数是2 | |
| C. | “打开电视,正在播放《新闻联播》”是必然事件 | |
| D. | 一组数据7,10,9,8,7的极差是3 |
14.如果两圆的半径分别为2cm和5cm,圆心距为6cm,那么这两个圆的位置关系是( )
| A. | 外离 | B. | 外切 | C. | 相交 | D. | 内切 |
11.下列说法正确的是( )
| A. | 单项式a的次数为0 | B. | 单项式a的系数为0 | ||
| C. | 多项式a4+a2的次数为6 | D. | 单项式πr2的次数为2 |

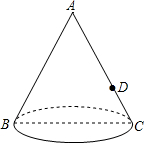 如图,圆锥的轴截面(过圆锥顶点和底面圆心的截面)是边长为2cm的等边△ABC,点D是AC的中点,一只蚂蚁从点B出发沿圆锥的表面爬行到点D处,则这只蚂蚁爬行的最短距离是$\sqrt{5}$cm.
如图,圆锥的轴截面(过圆锥顶点和底面圆心的截面)是边长为2cm的等边△ABC,点D是AC的中点,一只蚂蚁从点B出发沿圆锥的表面爬行到点D处,则这只蚂蚁爬行的最短距离是$\sqrt{5}$cm.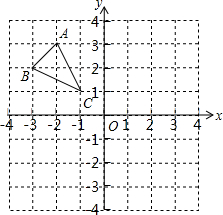 如图,在坐标系xOy中,A(-2,3),B(-3,2),C(-1,1),
如图,在坐标系xOy中,A(-2,3),B(-3,2),C(-1,1),