题目内容
12. 如图,在等腰三角形ABC中,AB=AC=15,点D在BC上,AB⊥AD,CD=7,则BD的长为18.
如图,在等腰三角形ABC中,AB=AC=15,点D在BC上,AB⊥AD,CD=7,则BD的长为18.
分析 延长BA至E,使BE=BA,结ED、EC,根据线段垂直平分线的性质得到BD=DE,由等腰三角形的性质得到∠ABD=∠AED,∠B=∠ACB,等量代换得到∠AED=∠ACB,推出A,D,C,E四点共圆,得到∠ECD=180°-∠EAD=90°=∠BAD,推出△BAD∽△BCA,根据相似三角形的性质得到$\frac{AB}{BC}=\frac{BD}{BE}$,即$\frac{15}{BD+7}=\frac{BD}{30}$,即可得到结论.
解答  解:延长BA至E,使BE=BA,结ED、EC
解:延长BA至E,使BE=BA,结ED、EC
∵AD⊥BE,
∴BD=DE,
∴∠ABD=∠AED,
∵AB=AC,
∴∠B=∠ACB,
∴∠AED=∠ACB,
∴A,D,C,E四点共圆,
∴∠EAD+∠ECD=180°,
∴∠ECD=180°-∠EAD=90°=∠BAD,
∴△BAD∽△BCA,
∴$\frac{AB}{BC}=\frac{BD}{BE}$,即$\frac{15}{BD+7}=\frac{BD}{30}$,
∴BD=18,(负值舍去),
∴BD=18.
故答案为:18.
点评 本题考查了等腰三角形的性质,相似三角形的判定和性质,四点共圆,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
1.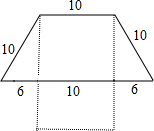 墙上钉着用一根彩绳围成的梯形形状的饰物,如图实线所示(单位:cm).小颖将梯形下底的钉子去掉,并将这条彩绳钉成一个长方形,如图虚线所示.小颖所钉长方形的长、宽各为多少厘米?如果设长方形的长为xcm,根据题意,可得方程为( )
墙上钉着用一根彩绳围成的梯形形状的饰物,如图实线所示(单位:cm).小颖将梯形下底的钉子去掉,并将这条彩绳钉成一个长方形,如图虚线所示.小颖所钉长方形的长、宽各为多少厘米?如果设长方形的长为xcm,根据题意,可得方程为( )
 墙上钉着用一根彩绳围成的梯形形状的饰物,如图实线所示(单位:cm).小颖将梯形下底的钉子去掉,并将这条彩绳钉成一个长方形,如图虚线所示.小颖所钉长方形的长、宽各为多少厘米?如果设长方形的长为xcm,根据题意,可得方程为( )
墙上钉着用一根彩绳围成的梯形形状的饰物,如图实线所示(单位:cm).小颖将梯形下底的钉子去掉,并将这条彩绳钉成一个长方形,如图虚线所示.小颖所钉长方形的长、宽各为多少厘米?如果设长方形的长为xcm,根据题意,可得方程为( )| A. | 2(x+10)=10×4+6×2 | B. | 2(x+10)=10×3+6×2 | C. | 2x+10=10×4+6×2 | D. | 2(x+10)=10×2+6×2 |
2.若抛物线y=ax2+bx+c与x轴的两个交点坐标是(-1,0)和(3,0),则抛物线的对称轴是( )
| A. | x=-1 | B. | x=-$\frac{1}{2}$ | C. | x=$\frac{1}{2}$ | D. | x=1 |
 如图,在△ABC中,∠ABC=60°,∠BAC、∠BCA的平分线相交于点O,求证:OE=OF.
如图,在△ABC中,∠ABC=60°,∠BAC、∠BCA的平分线相交于点O,求证:OE=OF. 如图所示,a⊥b,b∥c,∠1=120°,则∠2的度数是30°.
如图所示,a⊥b,b∥c,∠1=120°,则∠2的度数是30°.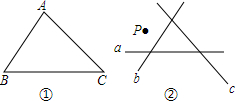 根据下列要求画图:
根据下列要求画图: