题目内容
20.在Rt△ABC中,a、b为直角边,c为斜边,若a+b=4,c=2$\sqrt{2}$,则△ABC的面积是2.分析 根据已知条件结合勾股定理列出方程求解即可.
解答 解:∵a+b=4,c=2$\sqrt{2}$,
∴(a+b)2=16,即a2+b2+2ab=16,
又∵a2+b2=c2=8,
∴2ab=8,
∴$\frac{1}{2}$ab=2,
即S△ABC=2,
故答案为:2.
点评 此题主要考查了勾股定理和三角形的面积公式的应用,能求出ab的值是解此题的关键.

练习册系列答案
相关题目
9.小明要到距家2000米的学校上学,一天小明出发8分钟后,他的爸爸从家出发,在距离学校200米的地方追上他,已知爸爸比小明的速度快80米/分,求小明的速度,若设小明的速度是x米/分,则根据题意所列方程正确的是( )
| A. | $\frac{1800}{x-80}$-$\frac{1800}{x}$=8 | B. | $\frac{1800}{x}$=8+$\frac{1800}{x-80}$ | ||
| C. | $\frac{1800}{x+80}$-$\frac{1800}{x}$=8 | D. | $\frac{1800}{x}$=8+$\frac{1800}{x+80}$ |
 如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=6cm,AB=8cm,BC=14cm.动点P、Q都从点C同时出发,点P沿C→B方向做匀速运动,点Q沿C→D→A方向做匀速运动,当P、Q其中一点到达终点时,另一点也随之停止运动.若点P以1cm/s速度运动,点Q以2$\sqrt{2}$cm/s的速度运动,连接BQ、PQ.当时间t为2秒时,△BQP的面积为24cm2.
如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=6cm,AB=8cm,BC=14cm.动点P、Q都从点C同时出发,点P沿C→B方向做匀速运动,点Q沿C→D→A方向做匀速运动,当P、Q其中一点到达终点时,另一点也随之停止运动.若点P以1cm/s速度运动,点Q以2$\sqrt{2}$cm/s的速度运动,连接BQ、PQ.当时间t为2秒时,△BQP的面积为24cm2.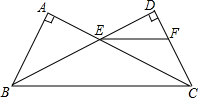 已知:如图,AB=DC,∠A=∠D=90°,AC,BD相交于点E,EF∥BC交CD于点F.求证:EF平分∠DEC.
已知:如图,AB=DC,∠A=∠D=90°,AC,BD相交于点E,EF∥BC交CD于点F.求证:EF平分∠DEC.
 如图,a∥b,∠2=70°,则∠1=110°.
如图,a∥b,∠2=70°,则∠1=110°. 如图,在等腰三角形ABC中,AB=AC=15,点D在BC上,AB⊥AD,CD=7,则BD的长为18.
如图,在等腰三角形ABC中,AB=AC=15,点D在BC上,AB⊥AD,CD=7,则BD的长为18. 实数a,b在数轴上的对应点如图所示,求代数式$\sqrt{{a}^{2}-2ab+{b}^{2}}$+|a+b|的值.
实数a,b在数轴上的对应点如图所示,求代数式$\sqrt{{a}^{2}-2ab+{b}^{2}}$+|a+b|的值.