题目内容
3. 如图,在△ABC中,∠ABC=60°,∠BAC、∠BCA的平分线相交于点O,求证:OE=OF.
如图,在△ABC中,∠ABC=60°,∠BAC、∠BCA的平分线相交于点O,求证:OE=OF.
分析 在CA上截取CG=CE,即可证明△CGO与△CEO全等,从而得到∠COG=∠COE,OE=OG;根据∠ABC=60°以及题目所给两条角平分线的条件,可算出∠AOC=120°,从而可得到∠AOF=∠AOG=∠COG=∠COE=60°,然后易证△AFO与△AGO全等,得到OG=OF,所以OF=OE.
解答 证明:在CA上截取CG=CE,如图,
在△CGO与△CEO中,
$\left\{\begin{array}{l}{CG=CE}\\{∠OCG=∠OCE}\\{OC=OC}\end{array}\right.$,
∴△CGO≌△CEO(SAS),
∴∠GOC=∠EOC,OE=OG
∵∠ABC=60°,AE平分∠BAC,CF平分∠BCA,
∴∠AOC=120°,
∴∠AOF=∠COE=∠COG=∠GOA=60°,
在△AFO与△AGO中,
$\left\{\begin{array}{l}{∠FAO=∠GAO}\\{AO=AO}\\{∠FOA=∠GOA}\end{array}\right.$,
∴△AFO≌△AGO(ASA),
∴OG=OF,
∴OE=OF.
点评 本题主要考查了全等三角形的判定与性质、三角形内角和性质,难度中等.根据角平分线的对称性,在两边截取线段相等构造三角形全等是重要技巧,要熟练掌握.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
13.某中学为了解学生一周在校的体育锻炼时问,随机地调查了50名宇生,结果如表所示:
则这50名学生这一周在校的平均体育锻炼时间是( )
| 时间(小时) | 5 | 6 | 7 | 8 |
| 人数 | 10 | 15 | 20 | 5 |
| A. | 6.2小时 | B. | 6.4小时 | C. | 6.5小时 | D. | 7小时 |
 如图,在△ABC中,∠A=62°,点O是AB,AC的垂直平分线的交点,则∠OCB的度数为28°.
如图,在△ABC中,∠A=62°,点O是AB,AC的垂直平分线的交点,则∠OCB的度数为28°. 如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=6cm,AB=8cm,BC=14cm.动点P、Q都从点C同时出发,点P沿C→B方向做匀速运动,点Q沿C→D→A方向做匀速运动,当P、Q其中一点到达终点时,另一点也随之停止运动.若点P以1cm/s速度运动,点Q以2$\sqrt{2}$cm/s的速度运动,连接BQ、PQ.当时间t为2秒时,△BQP的面积为24cm2.
如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=6cm,AB=8cm,BC=14cm.动点P、Q都从点C同时出发,点P沿C→B方向做匀速运动,点Q沿C→D→A方向做匀速运动,当P、Q其中一点到达终点时,另一点也随之停止运动.若点P以1cm/s速度运动,点Q以2$\sqrt{2}$cm/s的速度运动,连接BQ、PQ.当时间t为2秒时,△BQP的面积为24cm2. 如图,点P是直线l:y=-2x-2上的点,过点P的另一条直线m交抛物线y=x2于A、B两点,试证明:对于直线l上任意给定的一点P,在抛物线上都能找到点A,使得PA=AB成立.
如图,点P是直线l:y=-2x-2上的点,过点P的另一条直线m交抛物线y=x2于A、B两点,试证明:对于直线l上任意给定的一点P,在抛物线上都能找到点A,使得PA=AB成立.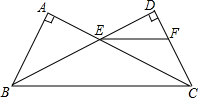 已知:如图,AB=DC,∠A=∠D=90°,AC,BD相交于点E,EF∥BC交CD于点F.求证:EF平分∠DEC.
已知:如图,AB=DC,∠A=∠D=90°,AC,BD相交于点E,EF∥BC交CD于点F.求证:EF平分∠DEC.
 如图,在等腰三角形ABC中,AB=AC=15,点D在BC上,AB⊥AD,CD=7,则BD的长为18.
如图,在等腰三角形ABC中,AB=AC=15,点D在BC上,AB⊥AD,CD=7,则BD的长为18.