题目内容
8.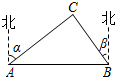 如图,A,B两市相距150千米,分别从A,B处测得风景区中心C处的方向角如图所示,风景区区域是以C为圆心,45千米为半径的圆.现计划修建连接A,B两市的笔直高速公路,此高速公路是否穿过风景区,请说明理由(tanα=1.627,tanβ=1.373).
如图,A,B两市相距150千米,分别从A,B处测得风景区中心C处的方向角如图所示,风景区区域是以C为圆心,45千米为半径的圆.现计划修建连接A,B两市的笔直高速公路,此高速公路是否穿过风景区,请说明理由(tanα=1.627,tanβ=1.373).
分析 首先过C作CD⊥AB与D,由题意得∠ACD=α,∠BCD=β,在Rt△ACD中,AD=CD•tanα,在Rt△BCD中,BD=CD•tanβ,继而可得CD•tanα+CD•tanβ=AB,则可求得CD的长,再进行比较,即可得出高速公路是否穿过风景区.
解答  解:AB不穿过风景区;
解:AB不穿过风景区;
如图,过C作CD⊥AB于D,
∴AD=CD•tanα;BD=CD•tanβ,
由AD+BD=AB,得CD•tanα+CD•tanβ=AB,
∴CD=$\frac{AB}{tanα+tanβ}$=$\frac{150}{1.627+1.373}$=$\frac{150}{3}$=50(千米),
∵CD=50>45,
∴高速公路AB不穿过风景区.
点评 此题考查了方向角问题.此题难度适中,注意能借助于方向角构造直角三角形,并利用解直角三角形的知识求解是解此题的关键.

练习册系列答案
相关题目
3. 如图,已知∠3=∠4,要得到AB∥CD,需要添加的条件是( )
如图,已知∠3=∠4,要得到AB∥CD,需要添加的条件是( )
 如图,已知∠3=∠4,要得到AB∥CD,需要添加的条件是( )
如图,已知∠3=∠4,要得到AB∥CD,需要添加的条件是( )| A. | ∠1=∠4 | B. | ∠3=∠2 | C. | ∠1=∠2 | D. | ∠1与∠2互补 |
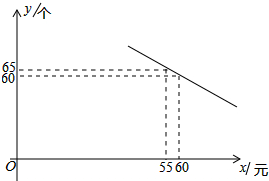 某体育用品商店试销一款成本为50元的排球,规定①试销售期三天;②试销期间单价不低于成本价,且获利不得高于40%.经试销发现,销售量y(个)与销售单价x(元)之间满足如图所示的一次函数关系.
某体育用品商店试销一款成本为50元的排球,规定①试销售期三天;②试销期间单价不低于成本价,且获利不得高于40%.经试销发现,销售量y(个)与销售单价x(元)之间满足如图所示的一次函数关系. 如图,在等腰梯形ABCD中,AD∥BC,AB=CD,∠A=120°,BD平分∠ABC,则∠BDC=90°.
如图,在等腰梯形ABCD中,AD∥BC,AB=CD,∠A=120°,BD平分∠ABC,则∠BDC=90°. 如图,AB是⊙O的直径,CD是⊙O的切线,切点为C,CD与AB的延长线相交于点D,∠CAD=20°,则∠D=50°.
如图,AB是⊙O的直径,CD是⊙O的切线,切点为C,CD与AB的延长线相交于点D,∠CAD=20°,则∠D=50°. 体育课上,老师用绳子围成一个周长30m的游戏场地,围成的场地是如图所示的矩形ABCD,设边AB的长为x(单位:m),矩形ABCD的面积为S(单位:m2).
体育课上,老师用绳子围成一个周长30m的游戏场地,围成的场地是如图所示的矩形ABCD,设边AB的长为x(单位:m),矩形ABCD的面积为S(单位:m2).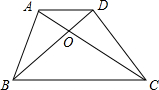 如图,四边形ABCD的对角线AC,BD相交于点0,且∠BAO=∠CDO,试问$\frac{AD}{BC}$=$\frac{AO}{BO}$成立吗?并说明理由.
如图,四边形ABCD的对角线AC,BD相交于点0,且∠BAO=∠CDO,试问$\frac{AD}{BC}$=$\frac{AO}{BO}$成立吗?并说明理由.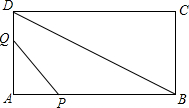 如图,矩形ABCD中AB=12cm,BC=6cm,点P沿AB边从点A开始以2cm/秒的速度移动,点Q沿DA边从D以1cm/秒的速度移动,若P、Q同时出发,用t表示移动时间(0≤t≤6),求当t何值时,△APQ与△ABC相似?
如图,矩形ABCD中AB=12cm,BC=6cm,点P沿AB边从点A开始以2cm/秒的速度移动,点Q沿DA边从D以1cm/秒的速度移动,若P、Q同时出发,用t表示移动时间(0≤t≤6),求当t何值时,△APQ与△ABC相似?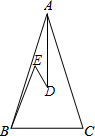 如图,在△ABC中,AB=AC,D、E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°,若BE=30cm,DE=2cm,则BC=32cm.
如图,在△ABC中,AB=AC,D、E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°,若BE=30cm,DE=2cm,则BC=32cm.