题目内容
13. 体育课上,老师用绳子围成一个周长30m的游戏场地,围成的场地是如图所示的矩形ABCD,设边AB的长为x(单位:m),矩形ABCD的面积为S(单位:m2).
体育课上,老师用绳子围成一个周长30m的游戏场地,围成的场地是如图所示的矩形ABCD,设边AB的长为x(单位:m),矩形ABCD的面积为S(单位:m2).(1)求S与x之间的函数关系式(不要求写出自变量x的取值范围);
(2)边AB的长取何值时,矩形ABCD的面积最大,最大面积是多少?
(3)若矩形ABCD的面积为50m2,且AB<AD,请求出此时AB的长.
分析 (1)根据长方形的面积公式求出S与x之间的函数关系式.
(2)根据二次函数的性质求出最值即可;
(3)根据矩形ABCD的面积为50平方米,即S=50,即可列出一元二次方程求解.
解答 解:(1)根据题意得:边AB的长为xm,
则AD=$\frac{30-2x}{2}$=15-x,
∴S=x(15-x)=-x2+15x;
(2)S=-x2+15x=-(x-$\frac{15}{2}$)2+$\frac{225}{4}$,
∴当边AB的长取7.5米时,矩形ABCD的面积最大,最大面积是$\frac{225}{4}$平方米;
(3)当S=50时,
-x2+15x=50,
整理得x2-15x+50=0,
解得x1=5,x2=10,
当AB=5时,AD=10;
当AB=10时,AD=5,
∵AB<AD,
∴AB=5,
故当矩形ABCD的面积为50平方米时AB的长为5米.
点评 本题主要考查了二次函数的应用,对于长方形的面积公式要熟记.注意本题AB<AD,因此可根据这个条件舍去不合题意的解.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 如图,△ABC≌△ADE,BC=DE,∠B=100°,∠BAC=40°那么∠AED=40°.
如图,△ABC≌△ADE,BC=DE,∠B=100°,∠BAC=40°那么∠AED=40°.
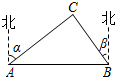 如图,A,B两市相距150千米,分别从A,B处测得风景区中心C处的方向角如图所示,风景区区域是以C为圆心,45千米为半径的圆.现计划修建连接A,B两市的笔直高速公路,此高速公路是否穿过风景区,请说明理由(tanα=1.627,tanβ=1.373).
如图,A,B两市相距150千米,分别从A,B处测得风景区中心C处的方向角如图所示,风景区区域是以C为圆心,45千米为半径的圆.现计划修建连接A,B两市的笔直高速公路,此高速公路是否穿过风景区,请说明理由(tanα=1.627,tanβ=1.373).