题目内容
如图△ABC中，AD⊥BC于D，AB=13，AD=12，BC=14，求AC的长．考点：勾股定理
专题：
分析：先根据勾股定理求出BD的长，进而可得出CD的长，再在Rt△ACD中，由勾股定理可得出AC的长．
解答：解：∵AD⊥BC于D，AB=13，AD=12，
∴BD=
=
=5．
∴CD=BC-BD=14-5=9．
在Rt△ACD中，
∵AD=12，CD=9，
∴AC=
=
=15．
∴BD=
| AB2-AD2 |
| 132-122 |
∴CD=BC-BD=14-5=9．
在Rt△ACD中，
∵AD=12，CD=9，
∴AC=
| AD2+CD2 |
| 122+92 |
点评：本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
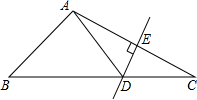如图，在△ABC中，DE是AC的垂直平分线，AE=4cm，△ABD的周长为15cm，求△ABC的周长．
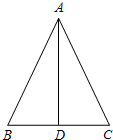如图，在△ABC中，AB=17，BC=16，BC边上的中线AD=15，
已知，如图∠C=∠ABD=90°，AC=4，BC=3，AD=13，则求BD的长度．
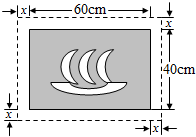在一幅长60cm、宽40cm的矩形风景画的四周外镶一条金色纸边，制成一幅矩形挂图，如图所示．如果要使整个挂图的面积是2816cm2，那么金色纸边的宽应为多少cm？
如图，直线y=kx-2与双曲线y=