题目内容
3.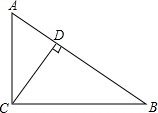 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,tan∠ACD=$\frac{3}{4}$,AB=5,那么CD的长是$\frac{12}{5}$.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,tan∠ACD=$\frac{3}{4}$,AB=5,那么CD的长是$\frac{12}{5}$.
分析 根据余角的性质得到∠B=∠ACD,由tan∠ACD=$\frac{3}{4}$,得到tan∠B=$\frac{AC}{BC}$=$\frac{3}{4}$,设AC=3x,BC=4x,根据勾股定理得到AC=3,BC=4,根据三角形的面积公式即可得到结论..
解答 解:∵∠ACB=90°,CD⊥AB,
∴∠ACD+∠BCD=∠BCD+∠B=90°,
∴∠B=∠ACD,
∵tan∠ACD=$\frac{3}{4}$,
∴tan∠B=$\frac{AC}{BC}$=$\frac{3}{4}$,
设AC=3x,BC=4x,
∵AC2+BC2=AB2,
∴(3x)2+(4x)2=52,
解得:x=1,
∴AC=3,BC=4,
∵S△ABC=$\frac{1}{2}AB•CD=\frac{1}{2}AC•BC$,
∴CD=$\frac{AC•BC}{AB}$=$\frac{12}{5}$,
故答案为:$\frac{12}{5}$.
点评 本题考查了解直角三角形,勾股定理,三角形的面积公式,熟记三角形的面积公式是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.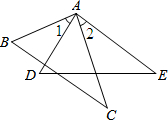 已知:如图,AB=AD,∠1=∠2,以下条件中,不能推出△ABC≌△ADE的是( )
已知:如图,AB=AD,∠1=∠2,以下条件中,不能推出△ABC≌△ADE的是( )
 已知:如图,AB=AD,∠1=∠2,以下条件中,不能推出△ABC≌△ADE的是( )
已知:如图,AB=AD,∠1=∠2,以下条件中,不能推出△ABC≌△ADE的是( )| A. | AE=AC | B. | ∠B=∠D | C. | BC=DE | D. | ∠C=∠E |
8.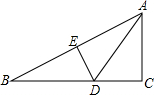 如图,△ABC中,∠ACB=90°,∠B=30°,DE垂直平分AB,若DE=1.5cm,则BC的长是( )
如图,△ABC中,∠ACB=90°,∠B=30°,DE垂直平分AB,若DE=1.5cm,则BC的长是( )
 如图,△ABC中,∠ACB=90°,∠B=30°,DE垂直平分AB,若DE=1.5cm,则BC的长是( )
如图,△ABC中,∠ACB=90°,∠B=30°,DE垂直平分AB,若DE=1.5cm,则BC的长是( )| A. | 3cm | B. | 4.5cm | C. | 6cm | D. | 7.5cm |
 已知:如图,直线m∥n.Rt△ABC与直线m、n分别相交,且∠1=25°,∠2=80°,求∠A的度数.
已知:如图,直线m∥n.Rt△ABC与直线m、n分别相交,且∠1=25°,∠2=80°,求∠A的度数. 如图,利用一面足够长的墙,用铁栅栏围成一个矩形自行车场地ABCD,在AB和BC边各有一个2米宽的小门(不用铁栅栏),设矩形ABCD的宽AD为x米,矩形的长为AB(且AB>AD).
如图,利用一面足够长的墙,用铁栅栏围成一个矩形自行车场地ABCD,在AB和BC边各有一个2米宽的小门(不用铁栅栏),设矩形ABCD的宽AD为x米,矩形的长为AB(且AB>AD).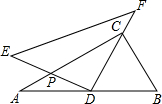 将一副三角尺如图摆放,其中在Rt△ABC中,∠ACB=90°,∠B=60°,在Rt△EDF中,∠EDF=90°,∠E=45°.点D为边AB的中点,DE交AC于点P,DF经过点C,将△EDF绕点D顺时针方向旋转角α(0°<α<60°)后得△E′DF′,DE′交AC于点M,DF′交BC于点N,那么$\frac{PM}{CN}$的值为$\frac{\sqrt{3}}{3}$.
将一副三角尺如图摆放,其中在Rt△ABC中,∠ACB=90°,∠B=60°,在Rt△EDF中,∠EDF=90°,∠E=45°.点D为边AB的中点,DE交AC于点P,DF经过点C,将△EDF绕点D顺时针方向旋转角α(0°<α<60°)后得△E′DF′,DE′交AC于点M,DF′交BC于点N,那么$\frac{PM}{CN}$的值为$\frac{\sqrt{3}}{3}$.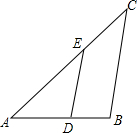 如图,已知△ABC∽△ADE,AE=5cm,EC=3cm,BC=7cm,∠BAC=45°,∠C=40°.
如图,已知△ABC∽△ADE,AE=5cm,EC=3cm,BC=7cm,∠BAC=45°,∠C=40°. 已知,如图,四边形ABCD中.AB=AD,CB=CD,AC与BD交于点E.求证:
已知,如图,四边形ABCD中.AB=AD,CB=CD,AC与BD交于点E.求证: