题目内容
7.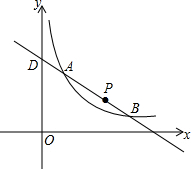 如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点A(2,5)和点B(m,1).
如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点A(2,5)和点B(m,1).(1)确定这两个函数的表达式;
(2)直线y=ax+b与x轴交于点C,与y轴交于点D,点P是线段CD上一动点,求点P到点O的最短距离.
分析 (1)根据函数图象上当的坐标特征求出m,得到两个函数的表达式;
(2)作OP⊥AB于P,根据勾股定理求出CD的长,根据三角形的面积公式计算即可.
解答 解:(1)∵点A(2,5)在反比例函数y=$\frac{k}{x}$(x>0)的图象上,
∴k=10,
则在反比例函数解析式为y=$\frac{10}{x}$,
∵点B(m,1)在反比例函数y=$\frac{10}{x}$的图象上,
∴m=10,
由题意得,$\left\{\begin{array}{l}{2a+b=5}\\{10a+b=1}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=6}\end{array}\right.$,
则一次函数解析式为:y=-$\frac{1}{2}$x+6;
(2)作OP⊥AB于P,
当x=0时,y=6,
∴y=-$\frac{1}{2}$x+6与y轴的交点D的坐标为:(0,6),
当y=0时,0=-$\frac{1}{2}$x+6,
解得,x=12,
则y=-$\frac{1}{2}$x+6与x轴的交点C的坐标为:(12,0),
∴CD=$\sqrt{O{D}^{2}+O{C}^{2}}$=6$\sqrt{5}$,
则$\frac{1}{2}$×CD×OP=$\frac{1}{2}$×OD×OC,即6$\sqrt{5}$×OP=72,
解得,OP=$\frac{12\sqrt{5}}{5}$.
点评 本题考查的是反比例函数与一次函数的交点问题,掌握待定系数法求函数解析式、正确求出反比例函数与一次函数的交点坐标是解题的关键.

练习册系列答案
相关题目
11.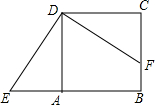 如图,正方形ABCD中,点F在边BC上,E在边BA的延长线上.∠CDF=30°,若△DCF按顺时针方向旋转后恰好与△DAE重合.则最少旋转了( )度.
如图,正方形ABCD中,点F在边BC上,E在边BA的延长线上.∠CDF=30°,若△DCF按顺时针方向旋转后恰好与△DAE重合.则最少旋转了( )度.
 如图,正方形ABCD中,点F在边BC上,E在边BA的延长线上.∠CDF=30°,若△DCF按顺时针方向旋转后恰好与△DAE重合.则最少旋转了( )度.
如图,正方形ABCD中,点F在边BC上,E在边BA的延长线上.∠CDF=30°,若△DCF按顺时针方向旋转后恰好与△DAE重合.则最少旋转了( )度.| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
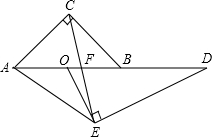 在等腰Rt△ABC中,∠ACB=90°,O是AB的中点,D在AB的延长线上,E在AD下方且∠OED=90°,∠OAE=∠OEA,CE交AD于F.
在等腰Rt△ABC中,∠ACB=90°,O是AB的中点,D在AB的延长线上,E在AD下方且∠OED=90°,∠OAE=∠OEA,CE交AD于F. P是正方形ABCD对角线AB上一点,若PC=AB,则∠BPC的大小为67.5度.
P是正方形ABCD对角线AB上一点,若PC=AB,则∠BPC的大小为67.5度.