题目内容
15. P是正方形ABCD对角线AB上一点,若PC=AB,则∠BPC的大小为67.5度.
P是正方形ABCD对角线AB上一点,若PC=AB,则∠BPC的大小为67.5度.
分析 根据正方形的性质可得出∠BCA=45°、AB=BC,结合PC=AB即可得出△BCP为等腰三角形,根据三角形的内角和定理以及等腰三角形的性质即可求出∠BPC的大小.
解答 解:∵四边形ABCD为正方形,AC为对角线,
∴∠BCA=∠BAC=45°,AB=BC.
∵PC=AB,
∴PC=BC,
∴△BCP为等腰三角形,
∴∠BPC=∠PBC=$\frac{1}{2}$(180°-∠BCP)=$\frac{1}{2}$×(150°-45°)=67.5°.
故答案为:67.5.
点评 本题考查了正方形的性质、等腰三角形的性质以及三角形内角和定理,解题的关键是找出△BCP为等腰三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
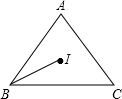 如图,在△ABC中,AB=AC=10,BC=12,I为△ABC的内心.
如图,在△ABC中,AB=AC=10,BC=12,I为△ABC的内心. 一次函数y=kx+b的图象如图,则当0≤x≤1时,y的范围是-2≤y<0.
一次函数y=kx+b的图象如图,则当0≤x≤1时,y的范围是-2≤y<0.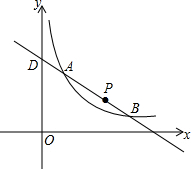 如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点A(2,5)和点B(m,1).
如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点A(2,5)和点B(m,1).