题目内容
16．已知二次函数y=2x2-3x+k的最小值是1，那么k的值为-$\frac{1}{8}$．分析 先把y=2x2-3x+k配成顶点式得到y=（x-2）2+k-4，根据二次函数的性质得到当x=2时，y有最小值为k-4，根据题意得k-4=1，然后解方程即可．
解答 解：y=2x2-3x+k
=2（x-$\frac{3}{4}$）2+k+$\frac{9}{8}$，
∵a=2＞0，
∴当x=$\frac{3}{4}$时，y有最小值为k+$\frac{9}{8}$，
∴k+$\frac{9}{8}$=1，
∴k=-$\frac{1}{8}$．
故答案为：-$\frac{1}{8}$．
点评 本题考查了二次函数的最值，把二次函数的一般式化成顶点式是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
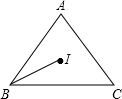如图，在△ABC中，AB=AC=10，BC=12，I为△ABC的内心．
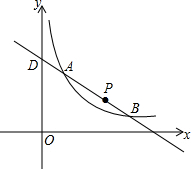如图，一次函数y=ax+b与反比例函数y=$\frac{k}{x}$（x＞0）的图象交于点A（2，5）和点B（m，1）．
如图，∠1+∠2=180°，∠3=65°，求∠4的度数．