��Ŀ����
�������Ķ�����������֤����Ȼ��������1?����3��
��֪����ͼ1����ABC�У���ACB=90�㣬��ABC=60�㣮�ֱ���AB��ACΪ�����������ȱߡ�ABD�͵ȱߡ�ACE������DE��AB�ڵ�F����֤��DF=EF��
����1���������֤�������У�ʹ���ˡ���֤�����֣�����ѡ���֤�������ɲ�д������
����2������ԭ���⣬���ȥ��������ACB=90�㣬�����������䣬��ͼ3����̽������DF=EF�Ƿ��������˵�����ɣ�
����3����ԭ����������ı����£���ͼ3��ABƽ�֡�DBC����ABD�ס�CAE���ٴ�̽������DF=EF�Ƿ��������˵�����ɣ�
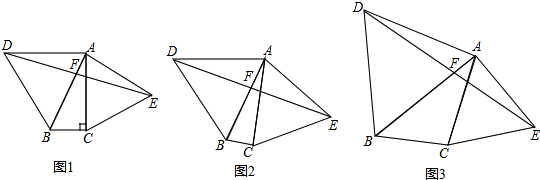
��֪����ͼ1����ABC�У���ACB=90�㣬��ABC=60�㣮�ֱ���AB��ACΪ�����������ȱߡ�ABD�͵ȱߡ�ACE������DE��AB�ڵ�F����֤��DF=EF��
����1���������֤�������У�ʹ���ˡ���֤�����֣�����ѡ���֤�������ɲ�д������
����2������ԭ���⣬���ȥ��������ACB=90�㣬�����������䣬��ͼ3����̽������DF=EF�Ƿ��������˵�����ɣ�
����3����ԭ����������ı����£���ͼ3��ABƽ�֡�DBC����ABD�ס�CAE���ٴ�̽������DF=EF�Ƿ��������˵�����ɣ�

���㣺ȫ�������ε��ж�������
ר�⣺
��������1����DG��AB����֤��ABC�ա�DBG���ɵ�DG=AC������֤����DGF�ա�EAF���ɵ�DF=EF��
��2����DG��AE������EG����֤��BAC=��BDG������֤����ABC�ա�DBG���ɵ�DG=AC�������ж��ı���AEGDΪƽ���ı��Σ����ɽ��⣻
��3����DG��AE����֤��EAF�ס�DGF���ɵ�
=
����֤��BDG�ס�BAC���ɵ�
=
�����ݡ�ABD�ס�CAE�ɵ�
=
�����ɽ��⣮
��2����DG��AE������EG����֤��BAC=��BDG������֤����ABC�ա�DBG���ɵ�DG=AC�������ж��ı���AEGDΪƽ���ı��Σ����ɽ��⣻
��3����DG��AE����֤��EAF�ס�DGF���ɵ�
| DG |
| AE |
| DF |
| EF |
| DG |
| AC |
| BD |
| AB |
| AB |
| BD |
| AC |
| AE |
���֤������1����DG��AB��

�ߡ�ABC�У���ACB=90�㣬��ABC=60�㣬
���BAC=30�㣬
�ߡ�ACE����BDGΪ�ȱ������Σ�
��AC=AE����CAE=60�㣬��ABD=60�㣬AB=BD��
���EAF=90�㣬��BDG=30�㣬
�ڡ�ABC�͡�DBG�У�
��
���ABC�ա�DBG����AAS����DG=AC����DG=AE��
�ڡ�DGF�͡�EAF�У�
��
���DGF�ա�EAF����AAS��
��DF=EF��
��2����DG��AE������EG��

�ߡ�ACE����BDGΪ�ȱ������Σ�
��AC=AE����CAE=60�㣬��ABD=60�㣬AB=BD��
��DG��AE��
���EAF=��DGF��
�ߡ�DGF=��ABD+��BDG����EAF=��CAE+��BAC�����BAC=��BDG��
�ڡ�ABC�͡�DBG�У�
��
���ABC�ա�DBG����AAS����DG=AC����DG=AE��
���ı���AEGDΪƽ���ı��Σ�
��DF=EF��
��3����DG��AE��

��DG��AE��
���EAF=��DGF����EAF�ס�DGF��
��
=
��
�ߡ�DGF=��ABD+��BDG����EAF=��CAE+��BAC�����BAC=��BDG��
��ABƽ�֡�DBC�����BDG�ס�BAC����
=
����DG=
��
��
=
��
�ߡ�ABD�ס�CAE��
��
=
��
��
=
=1����DF=EF��

�ߡ�ABC�У���ACB=90�㣬��ABC=60�㣬
���BAC=30�㣬
�ߡ�ACE����BDGΪ�ȱ������Σ�
��AC=AE����CAE=60�㣬��ABD=60�㣬AB=BD��
���EAF=90�㣬��BDG=30�㣬
�ڡ�ABC�͡�DBG�У�
|
���ABC�ա�DBG����AAS����DG=AC����DG=AE��
�ڡ�DGF�͡�EAF�У�
|
���DGF�ա�EAF����AAS��
��DF=EF��
��2����DG��AE������EG��

�ߡ�ACE����BDGΪ�ȱ������Σ�
��AC=AE����CAE=60�㣬��ABD=60�㣬AB=BD��
��DG��AE��
���EAF=��DGF��
�ߡ�DGF=��ABD+��BDG����EAF=��CAE+��BAC�����BAC=��BDG��
�ڡ�ABC�͡�DBG�У�
|
���ABC�ա�DBG����AAS����DG=AC����DG=AE��
���ı���AEGDΪƽ���ı��Σ�
��DF=EF��
��3����DG��AE��

��DG��AE��
���EAF=��DGF����EAF�ס�DGF��
��
| DG |
| AE |
| DF |
| EF |
�ߡ�DGF=��ABD+��BDG����EAF=��CAE+��BAC�����BAC=��BDG��
��ABƽ�֡�DBC�����BDG�ס�BAC����
| DG |
| AC |
| BD |
| AB |
| BD•AC |
| AB |
��
| DF |
| EF |
| BD•AC |
| AB•AE |
�ߡ�ABD�ס�CAE��
��
| AB |
| BD |
| AC |
| AE |
��
| DF |
| EF |
| BD•AC |
| AB•AE |
���������⿼����ȫ�������ε��ж���������ȫ�������ζ�Ӧ����ȵ����ʣ����������������ε��ж������ʣ���������֤��ABC�ա�DBG�͡�DGF�ա�EAF�ǽ���Ĺؼ���

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
 ��ͼ��PA��PB��CD�ֱ����O������A��B��E������COD=50�㣬���P=��������
��ͼ��PA��PB��CD�ֱ����O������A��B��E������COD=50�㣬���P=��������| A��80�� | B��55�� |
| C��130�� | D��65�� |
�����������������ƽ��3����λ��������ƽ��2����λ���ܵõ�������y=3x2���ǣ�������
| A��y=3��x+2��2+3 |
| B��y=3��x-2��2+3 |
| C��y=3��x+2��2-3 |
| D��y=3��x-2��2-3 |
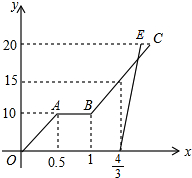 С�������г���С����Ħ�г�����ͬ·���ɼص��ҵأ�С���ȳ���������һ��ʱ��������г����ֹ��Ͻ���ά�ޣ��ú�ԭ�����ٶȼ������У�С���뿪��1Сʱ20�ֺ�С�ʼ���У���ͼ�����������뿪�صľ��루ǧ�ף��루Сʱ��֮��ĺ�����ϵͼ����֪С��������ٶ���С�ŵ�3����
С�������г���С����Ħ�г�����ͬ·���ɼص��ҵأ�С���ȳ���������һ��ʱ��������г����ֹ��Ͻ���ά�ޣ��ú�ԭ�����ٶȼ������У�С���뿪��1Сʱ20�ֺ�С�ʼ���У���ͼ�����������뿪�صľ��루ǧ�ף��루Сʱ��֮��ĺ�����ϵͼ����֪С��������ٶ���С�ŵ�3���� ��ͼ��������ͼ�У�С�����εı߳�1������ABC���������㶼�ڸ���ϣ�
��ͼ��������ͼ�У�С�����εı߳�1������ABC���������㶼�ڸ���ϣ�