题目内容
若（2x-y）2+2（2x-y）-3=0，则2x-y的值是（ ）
| A、1或-3 | B、-1或3 |
| C、1 | D、-3 |
考点：换元法解一元二次方程
专题：
分析：先设2x-y=z，则原方程变形为z2+2z-3=0，运用因式分解法解得z1=-3，z2=1，即可求得2x-y的值．
解答：解：设2x-y=z，则原方程变为：z2+2z-3=0，
分解因式，得（z+3）（z-1）=0，
解得，z1=-3，z2=1，
所以2x-y=-3或1．
故选A．
分解因式，得（z+3）（z-1）=0，
解得，z1=-3，z2=1，
所以2x-y=-3或1．
故选A．
点评：本题主要考查换元法在解一元二次方程中的应用．换元法是借助引进辅助元素，将问题进行转化的一种解题方法．这种方法在解题过程中，把某个式子看作一个整体，用一个字母去代表它，实行等量替换．这样做，常能使问题化繁为简，化难为易，形象直观．
练习册系列答案
相关题目
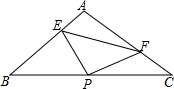如图Rt△ABC中，AB=AC=2，P是斜边BC中点，∠EPF两边分别交边AB、AC于E、F，且AF=BE．
如图，△ABC的内心为I，M、N分别是ABAC的中点，AB＞AC，内切圆⊙I与边BC，CA相切于D，E，证明：MN，BI，DE三线共点．