题目内容
8.定义感知:我们把具有对称轴和开口方向都相同的抛物线称作“同向共轴抛物线”.例如抛物线y=-3(x-2)2+3与y=-$\frac{1}{3}$(x-2)2-1的对称轴都是直线x=2,且开口方向都向下,则这两条抛物线称作“同向共轴抛物线”.初步运用:
(1)若抛物线y=3x2+mx-3与y=$\frac{1}{2}$x2-3x+5是“同向共轴抛物线”,则m=-18;
(2)若抛物线y=a1x2+b1x+c1与y=a2x2+b2x+c2是“同向共轴抛物线”,则下列结论正确的是②④⑤.(只须填上正确结论的顺序号即可)
①$\frac{{a}_{1}}{{a}_{2}}$=$\frac{{c}_{1}}{{c}_{2}}$;②$\frac{{a}_{1}}{{a}_{2}}$=$\frac{{b}_{1}}{{b}_{2}}$;③$\frac{{b}_{2}}{{b}_{1}}$=$\frac{{c}_{2}}{{c}_{1}}$;④$\frac{{a}_{1}^{2}}{{a}_{2}^{2}}$=$\frac{{b}_{1}^{2}}{{b}_{2}^{2}}$;⑤$\frac{{a}_{1}-{a}_{2}}{{a}_{2}}$=$\frac{{b}_{1}-{b}_{2}}{{b}_{2}}$.
拓展延伸:若抛物线y=ax2-x+c与y=$\frac{1}{2}$(x-3)2+1是“同向共轴抛物线”,且两抛物线的顶点相距3个单位长度,试求该抛物线的解析式.
分析 (1)根据同向共轴抛物线的定义列出关系式,求出m的值;
(2)根据对称轴相同的抛物线称作“同向共轴抛物线列式,根据比例的性质解答即可;
(2)根据同向共轴抛物线的定义求出a,根据二次函数的性质解答.
解答 解:(1)由同向共轴抛物线的定义可知,-$\frac{m}{2×3}$=-$\frac{-3}{2×\frac{1}{2}}$,
解得,m=-18,
故答案为:-18;
(2)∵抛物线y=a1x2+b1x+c1与y=a2x2+b2x+c2是“同向共轴抛物线”,
∴-$\frac{{b}_{1}}{2{a}_{1}}$=-$\frac{{b}_{2}}{2{a}_{2}}$,
∴$\frac{{a}_{1}}{{a}_{2}}$=$\frac{{b}_{1}}{{b}_{2}}$,②正确;
∴$\frac{{a}_{1}^{2}}{{a}_{2}^{2}}$=$\frac{{b}_{1}^{2}}{{b}_{2}^{2}}$,④正确;
由比例的性质可得,$\frac{{a}_{1}-{a}_{2}}{{a}_{2}}$=$\frac{{b}_{1}-{b}_{2}}{{b}_{2}}$,⑤正确;
由同向共轴抛物线的定义可知,同向共轴抛物线与c无关,
∴①③错误,
故答案为:②④⑤;
(3)由同向共轴抛物线的定义可知,-$\frac{-1}{2a}$=3,
解得,a=$\frac{1}{6}$,
y=$\frac{1}{6}$x2-x+c=$\frac{1}{6}$(x-3)2+c-$\frac{3}{2}$,
由题意得,c-$\frac{3}{2}$-1=±3,
解得,c=$\frac{11}{2}$或$-\frac{1}{2}$.
点评 本题考查的是待定系数法求函数解析式、同向共轴抛物线的定义,灵活运用待定系数法、掌握同向共轴抛物线的定义是解题的关键.

| 销售单价x(元) | … | 130 | 135 | 140 | 145 | … |
| 销售量y(件) | … | 240 | 230 | 220 | 210 | … |
(2)设商场所获利润为w元,将商品销售单价定为多少时,才能使所获利润最大?最大利润是多少?
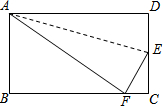 如图,折叠长方形纸片ABCD,使点D落在边BC上的点F处,折痕为AE.已知AB=6cm,BC=10cm.则EC的长为$\frac{8}{3}$cm.
如图,折叠长方形纸片ABCD,使点D落在边BC上的点F处,折痕为AE.已知AB=6cm,BC=10cm.则EC的长为$\frac{8}{3}$cm. 如图,己知双曲线y=$\frac{k}{x}$经过Rt△OAB斜边OB的中点D,与直角边AB相交于点C.若△OBC的面积为3,则k等于2.
如图,己知双曲线y=$\frac{k}{x}$经过Rt△OAB斜边OB的中点D,与直角边AB相交于点C.若△OBC的面积为3,则k等于2.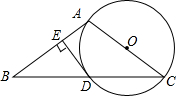 如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,过点D作DE⊥AB于点E.
如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,过点D作DE⊥AB于点E.