题目内容
1.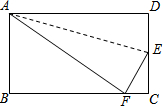 如图,折叠长方形纸片ABCD,使点D落在边BC上的点F处,折痕为AE.已知AB=6cm,BC=10cm.则EC的长为$\frac{8}{3}$cm.
如图,折叠长方形纸片ABCD,使点D落在边BC上的点F处,折痕为AE.已知AB=6cm,BC=10cm.则EC的长为$\frac{8}{3}$cm.
分析 根据长方形的性质可得AD=BC,根据翻转变换的性质可得AF=AD,EF=DE,利用勾股定理列式求出BF,再求出FC,然后设DE=x,表示出EC,在Rt△CEF中,利用勾股定理列方程求出x的值,即可解决问题.
解答 解:∵四边形ABCD是长方形,
∴AD=BC=10cm,CD=AB=6cm,
∵长方形纸片沿AE折叠,点D落在BC边的点F处,
∴AF=AD=10cm,EF=DE,
在Rt△ABF中,BF=$\sqrt{A{F}^{2}-A{B}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8cm,
∴FC=BC-BF=10-8=2cm,
设DE=x,则EC=CD-DE=6-x,
在Rt△CEF中,EC2+FC2=EF2,
即(6-x)2+22=x2,
解得x=$\frac{10}{3}$,
∴EC=CD-DE=6-$\frac{10}{3}$=$\frac{8}{3}$,
故答案为$\frac{8}{3}$.
点评 本题考查了翻转变换的性质,矩形的性质,勾股定理,翻折前后对应线段相等,对应角相等,此类题目,关键在于利用勾股定理列出方程.

练习册系列答案
相关题目
6. 如图,已知⊙O是△ABC的外接圆,若弦BC等于⊙O的半径,则∠BAC等于( )
如图,已知⊙O是△ABC的外接圆,若弦BC等于⊙O的半径,则∠BAC等于( )
 如图,已知⊙O是△ABC的外接圆,若弦BC等于⊙O的半径,则∠BAC等于( )
如图,已知⊙O是△ABC的外接圆,若弦BC等于⊙O的半径,则∠BAC等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 20° |
 如图,OB是∠AOC的角平分线,OD是∠COE的角平分线,如果∠AOB=40°,∠COE=60°,则∠BOD=70°.
如图,OB是∠AOC的角平分线,OD是∠COE的角平分线,如果∠AOB=40°,∠COE=60°,则∠BOD=70°.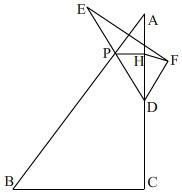 在△ABC中,∠ACB=Rt∠,BC=6,AC=8,点D是AC的中点,点P为AB边上的动点(P不与A重合),AP=t(t>0),PH⊥AC于点H,则PH=$\frac{3}{5}$t,连结DP并延长至点E,使得PE=PD,作点E关于AB的对称点F,连结FH.
在△ABC中,∠ACB=Rt∠,BC=6,AC=8,点D是AC的中点,点P为AB边上的动点(P不与A重合),AP=t(t>0),PH⊥AC于点H,则PH=$\frac{3}{5}$t,连结DP并延长至点E,使得PE=PD,作点E关于AB的对称点F,连结FH.