题目内容
10.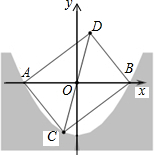 某水渠的横截面呈抛物线形,现以AB所在直线为x轴.以抛物线的对称轴为y轴建立如图所示的平面直角坐标系.已知水面的宽AB=8米,且抛物线解析式为y=ax2-4.
某水渠的横截面呈抛物线形,现以AB所在直线为x轴.以抛物线的对称轴为y轴建立如图所示的平面直角坐标系.已知水面的宽AB=8米,且抛物线解析式为y=ax2-4.(1)求a的值;
(2)点C(-1,m)是抛物线上一点,求点C关于原点O的对称点D;
(3)写出四边形ACBD的面积.
分析 (1)根据y轴为对称轴,AB=8,可得B(4,0),把B点坐标代入解析式即可求得a的值;
(2)根据(1)求得a的值,求出解析式,把C点坐标代入求得m的值,然后根据D、C关于原点对称求出D点坐标;
(3)根据四边形ACBD的面积=4S△BOD求出面积即可.
解答 解:(1)根据题意得:OA=OB=$\frac{1}{2}$AB=4,
∴B点坐标(4,0)
∴0=16a-4,
解得:a=$\frac{1}{4}$
∴此二次函数的解析式为:y=$\frac{1}{4}$x2-4.
(2)∵点C(一1,m)是抛物线上一点
∴m=$\frac{1}{4}$-4=-$\frac{15}{4}$,
又∵点D与点C关于原点中心对称
∴D点坐标(1,$\frac{15}{4}$).
(3)S四边形ACBD=4×$\frac{1}{2}$×4×$\frac{15}{4}$=30.
点评 本题考查了二次函数的应用,难度适中,解答本题的关键是熟练掌握用待定系数法函数解析式.

练习册系列答案
相关题目
1.在△ABC中,两中线AD与CF相交于点G,若∠AFC=45°,∠AGC=60°,则∠ACF的度数为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
5.王老师要选择两名同学担任九年级毕业典礼主持人.现有2名男同学和3名女同学候选,那么王老师选择一名男同学和一名女同学担任主持人的概率为( )
| A. | $\frac{2}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{5}{9}$ |
15.等腰三角形一腰上的高与另一腰的夹角为20°,则顶角的度数为( )
| A. | 70° | B. | 55° | C. | 110° | D. | 70°或110° |
2.下列函数中,一次函数的个数是:( )
①y=$\frac{1}{3}$ x;②y=-2+5x;③y=-$\frac{1}{x}$;④y=(2x-1)2+2;⑤y=$\frac{2}{3}$x-2;⑥y=2πx.
①y=$\frac{1}{3}$ x;②y=-2+5x;③y=-$\frac{1}{x}$;④y=(2x-1)2+2;⑤y=$\frac{2}{3}$x-2;⑥y=2πx.
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 1个 |
19.下列计算正确的是( )
| A. | a+2a=3a2 | B. | (-a2)3=a6 | C. | (-2a)2=4a2 | D. | a10÷a2=a5 |
20.下列商标是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |