题目内容
11.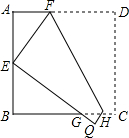 如图,将边长为6cm的正方形ABCD折叠,使点D落在AB边的中点E处,折痕为FH,点C落在Q处,EQ与BC交于点G,则△EBG的周长是12cm.
如图,将边长为6cm的正方形ABCD折叠,使点D落在AB边的中点E处,折痕为FH,点C落在Q处,EQ与BC交于点G,则△EBG的周长是12cm.
分析 设AF=x,则DF=6-x,由折叠的性质可知:EF=DF=6-x,在Rt△AFE,由勾股定理可求得:x=$\frac{9}{4}$,然后再证明△FAE∽△EBG,从而可求得BG=4,接下来在Rt△EBG中,由勾股定理可知:EG=5,从而可求得△EBG的周长为12cm.
解答 解:设AF=x,则DF=6-x,由折叠的性质可知:EF=DF=6-x.
在Rt△AFE,由勾股定理可知:EF2=AF2+AE2,即(6-x)2=x2+32,
解得:x=$\frac{9}{4}$.
∵∠FEG=90°,
∴∠AEF+∠BEG=90°.
又∵∠BEG+∠BGE=90°,
∴∠AEF=∠BGE.
又∵∠EAF=∠EBG,
∴△FAE∽△EBG.
∴$\frac{AF}{AE}=\frac{BE}{BG}$,即$\frac{\frac{9}{4}}{3}=\frac{3}{BG}$.
∴BG=4.
在Rt△EBG中,由勾股定理可知:EG=$\sqrt{B{E}^{2}+G{B}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5.
所以△EBG的周长=3+4+5=12cm.
点评 本题主要考查的是折叠的性质、勾股定理、相似三角形的综合应用,利用勾股定理求得AF的长是解题的关键.

练习册系列答案
相关题目
1.在△ABC中,两中线AD与CF相交于点G,若∠AFC=45°,∠AGC=60°,则∠ACF的度数为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
2.下列函数中,一次函数的个数是:( )
①y=$\frac{1}{3}$ x;②y=-2+5x;③y=-$\frac{1}{x}$;④y=(2x-1)2+2;⑤y=$\frac{2}{3}$x-2;⑥y=2πx.
①y=$\frac{1}{3}$ x;②y=-2+5x;③y=-$\frac{1}{x}$;④y=(2x-1)2+2;⑤y=$\frac{2}{3}$x-2;⑥y=2πx.
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 1个 |
19.下列计算正确的是( )
| A. | a+2a=3a2 | B. | (-a2)3=a6 | C. | (-2a)2=4a2 | D. | a10÷a2=a5 |
3.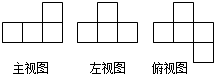 如图是由一些完全相同的小立方块搭成的几何体的三种视图.搭成这个几何体所用的小立方块的个数是( )
如图是由一些完全相同的小立方块搭成的几何体的三种视图.搭成这个几何体所用的小立方块的个数是( )
 如图是由一些完全相同的小立方块搭成的几何体的三种视图.搭成这个几何体所用的小立方块的个数是( )
如图是由一些完全相同的小立方块搭成的几何体的三种视图.搭成这个几何体所用的小立方块的个数是( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
20.下列商标是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
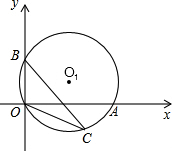 如图,在平面直角坐标系中,过点O的⊙O1与两坐标轴分别交于A、B两点A(4,0),B(0,2),点C在弧OA上,则tan∠BCO为$\frac{1}{2}$.
如图,在平面直角坐标系中,过点O的⊙O1与两坐标轴分别交于A、B两点A(4,0),B(0,2),点C在弧OA上,则tan∠BCO为$\frac{1}{2}$.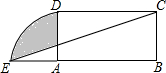 如图,在矩形ABCD中,AB=8cm,BC=4cm,以点A为圆心,AD为半径作圆与BA的延长线交于点E,连接CE,则阴影部分的面积是4π-$\frac{8}{3}$cm2.
如图,在矩形ABCD中,AB=8cm,BC=4cm,以点A为圆心,AD为半径作圆与BA的延长线交于点E,连接CE,则阴影部分的面积是4π-$\frac{8}{3}$cm2.