题目内容
5. 如图所示,在Rt△ABC中,∠C=90°,∠BAC=60°,AB=8.半径为$\sqrt{3}$的⊙M与射线BA相切,切点为N,且AN=3.将Rt△ABC顺时针旋转120°后得到Rt△ADE,点B、C的对应点分别是点D、E.此时Rt△ADE的斜边AD所在的直线与⊙M的位置关系是相切.
如图所示,在Rt△ABC中,∠C=90°,∠BAC=60°,AB=8.半径为$\sqrt{3}$的⊙M与射线BA相切,切点为N,且AN=3.将Rt△ABC顺时针旋转120°后得到Rt△ADE,点B、C的对应点分别是点D、E.此时Rt△ADE的斜边AD所在的直线与⊙M的位置关系是相切.
分析 过M作AD的垂线,设垂足为H,然后证MH与⊙M半径的大小关系即可;连接AM、MN,由于AE是⊙M的切线,故MN⊥AE,在Rt△AMN中,通过解直角三角形,易求得∠MAN=30°,由此可证得AM是∠DAE的角平分线,根据角平分线的性质即可得到MH=MN,由此可证得⊙M与AD相切.
解答 解:AD与⊙M相切.理由如下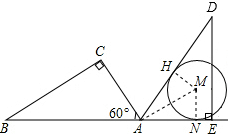
由旋转的性质得:∠DAE=∠BAC=60°,
过点M作MH⊥AD于H,连接MN,MA,则MN⊥AE,且MN=$\sqrt{3}$,
在Rt△AMN中,tan∠MAN=$\frac{MN}{AN}$=$\frac{\sqrt{3}}{3}$,∴∠MAN=30°,
∵∠DAE=∠BAC=60°,
∴∠MAD=30°,
∴∠MAN=∠MAD=30°,
∴MH=MN,
∴直线AD与⊙M相切.
故答案为:相切.
点评 本题主要考查了切线的判定方法、三角函数、角平分线的性质、旋转的性质;熟练掌握旋转的性质,证明MH=MN是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
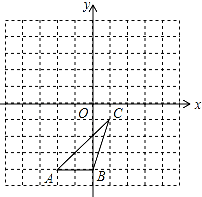 如图,△ABC各顶点的坐标分别是A(-2,-4),B(0,-4),C(1,-1)
如图,△ABC各顶点的坐标分别是A(-2,-4),B(0,-4),C(1,-1)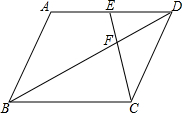 如图,在?ABCD中,F是对角线BD上的一点,连接CF并延长交AD于点E.若$\frac{BF}{DF}$=$\frac{1}{n}$,则$\frac{EF}{EC}$=n:(n+1).
如图,在?ABCD中,F是对角线BD上的一点,连接CF并延长交AD于点E.若$\frac{BF}{DF}$=$\frac{1}{n}$,则$\frac{EF}{EC}$=n:(n+1).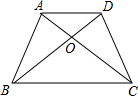 如图,四边形ABCD,AD∥BC,对角线AC,BD相交于点O,△AOD和△ABO的面积分别为2cm2和3cm2,求四边形ABCD的面积.
如图,四边形ABCD,AD∥BC,对角线AC,BD相交于点O,△AOD和△ABO的面积分别为2cm2和3cm2,求四边形ABCD的面积.