题目内容
17.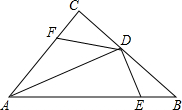 如图,已知:在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,点F在AC上.BD=DF.
如图,已知:在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,点F在AC上.BD=DF.(1)求证:CF=EB;
(2)请你判断EB+DC与DF的大小关系,并证明你的结论.
分析 (1)由角平分线的性质可知:DC=DE,然后由HL证明△CFD≌△EBD,由全等三角形的性质可知CF=EB;
(2)BE+CD=BE+ED>DB,由BD=DF可知:BE+CD>DF.
解答 解:(1)∵∠C=90°,
∴DC⊥AC.
∵AD平分∠BAC,DE⊥AB,DC⊥AC,
∴DC=DE.
在Rt△CFD和Rt△EBD中,
$\left\{\begin{array}{l}{DC=DE}\\{DF=DB}\end{array}\right.$,
∴Rt△CFD≌Rt△EBD,
∴CF=EB.
(2)∵DC=DE,
∴BE+CD=BE+ED.
∵BE+ED>DB,BD=DF,
∴BE+CD>DF.
点评 本题主要考查的全等三角形的性质和判定、角平分线的性质、三角形的三边关系,证得Rt△CFD≌Rt△EBD是解题的关键.

练习册系列答案
相关题目
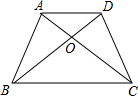 如图,四边形ABCD,AD∥BC,对角线AC,BD相交于点O,△AOD和△ABO的面积分别为2cm2和3cm2,求四边形ABCD的面积.
如图,四边形ABCD,AD∥BC,对角线AC,BD相交于点O,△AOD和△ABO的面积分别为2cm2和3cm2,求四边形ABCD的面积.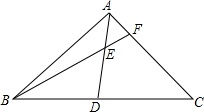 如图,在△ABC中,D是BC边的中点,E是AD上一点,BE=AC,BE的延长线交AC于F,求证:∠AEF=∠EAF.
如图,在△ABC中,D是BC边的中点,E是AD上一点,BE=AC,BE的延长线交AC于F,求证:∠AEF=∠EAF.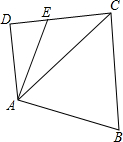 如图,E是四边形ABCD的DC边上一点,CE=$\sqrt{2}$,AB=2,BC=$\sqrt{3}+1$,∠D=90°,∠B=60°,S四边形ABCE=$\frac{3+2\sqrt{3}}{2}$
如图,E是四边形ABCD的DC边上一点,CE=$\sqrt{2}$,AB=2,BC=$\sqrt{3}+1$,∠D=90°,∠B=60°,S四边形ABCE=$\frac{3+2\sqrt{3}}{2}$ 如图,在△ABC中,∠ACB=90°,AC=BC=1,E,F是线段AB上的两个动点,且∠ECF=45°,过点E,F分别作BC,AC的垂线相交于点M,垂足分别为H,G.有以下结论:①AB=$\sqrt{2}$;②当点E与点B重合时,MH=$\frac{1}{2}$;③△ACE∽△BFC;④AF+BE=EF.其中正确的结论有( )
如图,在△ABC中,∠ACB=90°,AC=BC=1,E,F是线段AB上的两个动点,且∠ECF=45°,过点E,F分别作BC,AC的垂线相交于点M,垂足分别为H,G.有以下结论:①AB=$\sqrt{2}$;②当点E与点B重合时,MH=$\frac{1}{2}$;③△ACE∽△BFC;④AF+BE=EF.其中正确的结论有( ) 将图中平面展开图折叠成正方体后,相对面上的两个数互为相反数,则x+y+z=-1.5.
将图中平面展开图折叠成正方体后,相对面上的两个数互为相反数,则x+y+z=-1.5.


