题目内容
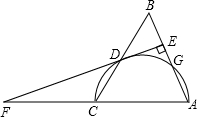 如图,AB=AC=4,以AC为直径的半圆⊙0交BC于点D,交AB于点G,DE⊥AB于点E,ED的延长线与AC的延长线交于点F,BE=1.
如图,AB=AC=4,以AC为直径的半圆⊙0交BC于点D,交AB于点G,DE⊥AB于点E,ED的延长线与AC的延长线交于点F,BE=1.(1)求证:直线EF是半圆⊙O的切线;
(2)求sinF的值.
考点:切线的判定
专题:证明题
分析:(1)连接OD,如图,由AB=AC得∠B=∠ACB,由OC=OD得∠OCD=∠ODC,则∠ODC=∠B,于是可判断OD∥AB,而DE⊥AB,所以DE⊥OD,然后根据切线的性质得到直线EF是半圆⊙O的切线;
(2)设FC=x,证明△FOD∽△FAE,利用相似比得到
=
,解得x=2,则FA=FC+AC=6,然后根据正弦的定义求解.
(2)设FC=x,证明△FOD∽△FAE,利用相似比得到
| 2 |
| 3 |
| x+2 |
| x+4 |
解答: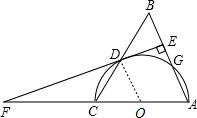 (1)证明:连接OD,如图,
(1)证明:连接OD,如图,
∵AB=AC,
∴∠B=∠ACB,
∵OC=OD,
∴∠OCD=∠ODC,
∴∠ODC=∠B,
∴OD∥AB,
∵DE⊥AB,
∴DE⊥OD,
∴直线EF是半圆⊙O的切线;
(2)解:设FC=x,
∵AB=AC=4,BE=1,
∴AE=3,OD=2,
∵OD∥AE,
∴△FOD∽△FAE,
∴
=
,即
=
,
解得x=2,
∴FA=FC+AC=2+4=6,
∴sin∠F=
=
=
.
 (1)证明:连接OD,如图,
(1)证明:连接OD,如图,∵AB=AC,
∴∠B=∠ACB,
∵OC=OD,
∴∠OCD=∠ODC,
∴∠ODC=∠B,
∴OD∥AB,
∵DE⊥AB,
∴DE⊥OD,
∴直线EF是半圆⊙O的切线;
(2)解:设FC=x,
∵AB=AC=4,BE=1,
∴AE=3,OD=2,
∵OD∥AE,
∴△FOD∽△FAE,
∴
| OD |
| AE |
| FO |
| FA |
| 2 |
| 3 |
| x+2 |
| x+4 |
解得x=2,
∴FA=FC+AC=2+4=6,
∴sin∠F=
| AE |
| AF |
| 3 |
| 6 |
| 1 |
| 2 |
点评:本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了锐角三角形函数和相似三角形的判定与性质.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
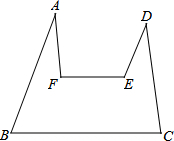 如图,顺次连结A、B、C、D、E、F,若∠F=∠A+∠B.求证:∠E=∠D+∠C.
如图,顺次连结A、B、C、D、E、F,若∠F=∠A+∠B.求证:∠E=∠D+∠C.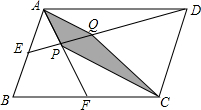 如图,E、F分别是平行四边形ABCD的边AB、BC的中点,DE与AF交于点P,点Q在线段DE上,且AQ∥PC,求梯形APCQ的面积与平行四边形ABCD的面积的比值.
如图,E、F分别是平行四边形ABCD的边AB、BC的中点,DE与AF交于点P,点Q在线段DE上,且AQ∥PC,求梯形APCQ的面积与平行四边形ABCD的面积的比值.