题目内容
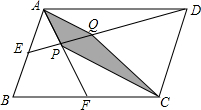如图，E、F分别是平行四边形ABCD的边AB、BC的中点，DE与AF交于点P，点Q在线段DE上，且AQ∥PC，求梯形APCQ的面积与平行四边形ABCD的面积的比值．考点：面积及等积变换
专题：
分析：首先连接EF，BP，AC，DF，设S?ABCD=a，由E、F分别是平行四边形ABCD的边AB、BC的中点，易求得S△ADE=S△ABF=
，继而可得EP：PD=1：4，然后设S△AEP=x，则S△ADP=4x，由S△APD=S四边形BEPF，可得
-x=4x，即可求得△AEP与△APD的面积，又由AQ∥PC，继而求得各部分的面积，即可求得答案．
| a |
| 4 |
| a |
| 4 |
解答：解：连接EF，BP，AC，DF，
设S?ABCD=a，
∵E、F分别是平行四边形ABCD的边AB、BC的中点，
∴S△ADE=S△ABF=
，
∴S△APD=S四边形BEPF，
∵S△AEF=
，S△ADF=
，
∴
=
=
，
设S△AEP=x，则S△ADP=4x，
∵S△APD=S四边形BEPF，
∴
-x=4x，
解得：x=
，
∴S△APD=4×
=
，
∵AQ∥PC，
∴S△APQ=S△ACQ，
∴S△ACQ+S△ADQ=
，
∴S△CDQ=
-
=
，
∵S△EBP=S△AEP=
，S△ABP+S△CDP=
，
∴S△APD=
-S△ABP-S△CDQ=
-
-
=
，
∴
=
=
=
，
∴
=
，
∴S△APQ=
S△APD=
，
∴S梯形APCQ=S△APQ+S△CPQ=
+
=
，
∴
=
．
设S?ABCD=a，
∵E、F分别是平行四边形ABCD的边AB、BC的中点，
∴S△ADE=S△ABF=
| a |
| 4 |
∴S△APD=S四边形BEPF，
∵S△AEF=
| a |
| 8 |
| a |
| 2 |
∴
| EP |
| PD |
| ||
|
| 1 |
| 4 |
设S△AEP=x，则S△ADP=4x，∵S△APD=S四边形BEPF，
∴
| a |
| 4 |
解得：x=
| a |
| 20 |
∴S△APD=4×
| a |
| 20 |
| a |
| 5 |
∵AQ∥PC，
∴S△APQ=S△ACQ，
∴S△ACQ+S△ADQ=
| a |
| 5 |
∴S△CDQ=
| a |
| 2 |
| a |
| 5 |
| 3a |
| 10 |
∵S△EBP=S△AEP=
| a |
| 20 |
| a |
| 2 |
∴S△APD=
| a |
| 2 |
| a |
| 2 |
| a |
| 10 |
| 3a |
| 10 |
| a |
| 10 |
∴
| PQ |
| PD |
| S△CPQ |
| S△CQD |
| ||
|
| 1 |
| 3 |
∴
| PQ |
| PD |
| 1 |
| 4 |
∴S△APQ=
| 1 |
| 4 |
| a |
| 20 |
∴S梯形APCQ=S△APQ+S△CPQ=
| a |
| 20 |
| a |
| 10 |
| 3a |
| 20 |
∴
| S梯形APCQ |
| S平行四边形ABCD |
| 3 |
| 20 |
点评：此题考查了面积与等积变换的知识．此题难度较大，注意等高三角形面积的比等于其对应底的比的性质的应用，注意掌握辅助线的作法，注意掌握数形结合思想与方程思想的应用．
练习册系列答案
名校课堂系列答案
相关题目
如图，在Rt△ABC中，∠ABC=90°，D、E在AC上，且AB=AD，CB=CE．求∠EBD的度数．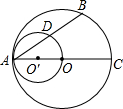
如图，OA是⊙O的半径，AB是⊙O的弦，以OA为直径的圆与AB相交于点D，
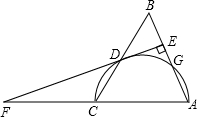如图，AB=AC=4，以AC为直径的半圆⊙0交BC于点D，交AB于点G，DE⊥AB于点E，ED的延长线与AC的延长线交于点F，BE=1．