题目内容
11. 已知有理数a,b,c在数轴上的位置如图所示,请化简:
已知有理数a,b,c在数轴上的位置如图所示,请化简:(1)|-a|-|b-a|+|c-a|-|a+b|;
(2)|a+c|-|1-b|+|-a-b|;
(3)|a|-|a+c|+|b|+|a-b+c|.
分析 原式各项根据数轴上点的位置判断出绝对值里边式子的正负,利用绝对值的代数意义化简,去括号合并即可得到结果.
解答 解:(1)由数轴上点的位置得:c<a<0<b<1,
则-a>0,b-a>0,c-a<0,a+b<0,
则原式=-a-b+a+a-c+a+b=2a-c;
(2)根据题意得:a+c<0,1-b>0,-a-b>0,
则原式=-a-c-1+b-a-b=-2a-c-1;
(3)根据题意得:a+c<0,a-b+c<0,
则原式=-a+a+c+b-a+b-c=-a+2b.
点评 此题考查了整式的加减,数轴,以及绝对值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.下列式子成立的是( )
| A. | $\frac{b}{a}$+$\frac{2}{b}$=$\frac{b+2}{a+b}$ | B. | ($\frac{-y}{2x}$)2=$\frac{{y}^{2}}{2x}$ | C. | y2÷y-3=y-1 | D. | $\frac{a}{a-b}$-$\frac{b}{a-b}$=1 |
2.关于x,y的二元一次方程组$\left\{\begin{array}{l}x+y=0\\ x-y=2k\end{array}\right.$的解也是二元一次方程2011x+2012y=2013的解,则k的值为( )
| A. | 2012 | B. | -2012 | C. | 2013 | D. | -2013 |
6.已知二次函数y=x2+bx+c中,函数y与自变量x的部分对应值如下表:
(1)求该二次函数的关系式;
(2)当x为何值时,y有最小值,最小值是多少?
(3)若A(m,y1),B(m+1,y2)两点都在该函数的图象上,其中m<1,试比较y1与y2的大小.
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 10 | 5 | 2 | 1 | 2 | 5 | … |
(2)当x为何值时,y有最小值,最小值是多少?
(3)若A(m,y1),B(m+1,y2)两点都在该函数的图象上,其中m<1,试比较y1与y2的大小.
 如图,E为△ABC中AB边的中点,D为△ABC外一点,且DE⊥AB,过点D作DN⊥AC于点N,DM⊥BC交BC的延长线于点M,已知AN=BM,求证:点D在△ABC的外角平分线上.
如图,E为△ABC中AB边的中点,D为△ABC外一点,且DE⊥AB,过点D作DN⊥AC于点N,DM⊥BC交BC的延长线于点M,已知AN=BM,求证:点D在△ABC的外角平分线上.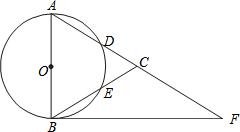 如图,在△ABC中,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且AC=CF,∠CBF=∠CFB.
如图,在△ABC中,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且AC=CF,∠CBF=∠CFB.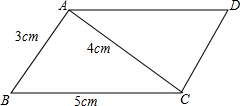 求如图所示的平行四边形ABCD的面积=12cm2.
求如图所示的平行四边形ABCD的面积=12cm2.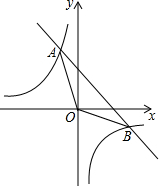 一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于A(-1,$\sqrt{3}$)、B($\sqrt{3}$,n)两点.
一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于A(-1,$\sqrt{3}$)、B($\sqrt{3}$,n)两点. 如图,已知一次函数y=k1x+b的图象与反比例函数y=$\frac{k_2}{x}$的图象交于A(1,-2),B(2,m)两点,连接OA、OB.
如图,已知一次函数y=k1x+b的图象与反比例函数y=$\frac{k_2}{x}$的图象交于A(1,-2),B(2,m)两点,连接OA、OB.