题目内容
1．
如图，已知一次函数y=k1x+b的图象与反比例函数y=$\frac{k_2}{x}$的图象交于A（1，-2），B（2，m）两点，连接OA、OB．（1）求两个函数的解析式；
（2）求△AOB的面积．
分析 （1）首先把A（1，-2）代入反比例函数解析式中确定k2，然后把B（2，m）代入反比例函数的解析式确定m，然后根据A，B两点坐标利用待定系数法确定一次函数的解析式；
（2）根据一次函数解析式求出其图象与坐标轴的交点坐标，然后用面积的割补法可以求出△ABO的面积．
解答 解：（1）把A（1，-2）代入y=$\frac{{k}_{2}}{x}$中，
解得：k2=-2，
故y=-$\frac{2}{x}$，
把B（2，m）代入y=-$\frac{2}{x}$，解得m=-1，
故B（2，-1），
把A（1，-2），B（2，-1）代入y=k1x+b
得$\left\{\begin{array}{l}{-2=k+b}\\{-1=2k+b}\end{array}\right.$，解得：$\left\{\begin{array}{l}{k=1}\\{b=-3}\end{array}\right.$，
故一次函数解析式为y=x-3．
（2）当x=0时，y=-3．当y=0时，x=3，所以直线AB与坐标轴的交点坐标为C（3，0），D（0，-3）
故S△OAB=S△AOC-S△BOC=3．
点评 此题考查了用待定系数法确定反比例函数和一次函数的解析式，也考查了利用函数的性质求不规则图形的面积．
练习册系列答案
相关题目
已知有理数a，b，c在数轴上的位置如图所示，请化简：
如图，?ABCD中，AC、BD交于点O1，作?BCD1O1，连结BD1交AC于点O2，作?BCD2O2，连结BD2交AC于点O3，…以此类推，若AC⊥AD，AD=1，∠ADC=60°，则?BCDnOn的面积是$\frac{\sqrt{3}}{{2}^{n}}$．
已知反比例函数y=$\frac{k}{x}$图象过第二象限内的点A（-2，m），AB⊥x轴于B，Rt△AOB面积为3，若直线y=ax+b经过点A，并且经过反比例函数y=$\frac{k}{x}$的图象上另一点C（n，-1），
如图，△ABC中，DF平分∠BDE，EF平分∠DEC，求证：AF平分∠BAC．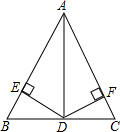
如图，在△ABC中，AD平分∠BAC交BC于D，DE⊥AB于E，DF⊥AC于F，EB=FC．求证：BD=CD．