题目内容
12.有下面四个等式:(1)$\sqrt{2+\frac{2}{3}}$=$2\sqrt{\frac{2}{3}}$;
(2)$\sqrt{3+\frac{3}{8}}$=$3\sqrt{\frac{3}{8}}$;
(3)$\sqrt{4+\frac{4}{15}}$=$4\sqrt{\frac{4}{15}}$;
(4)$\sqrt{5+\frac{5}{24}}=5\sqrt{\frac{4}{25}}$
观察上面四个等式,发现了什么规律,请用含有n(n是正整数,且n>1)的代数式将规律表示出来$\sqrt{a+\frac{a}{{a}^{2}-1}}$=a$\sqrt{\frac{a}{{a}^{2}-1}}$.
分析 直接利用已知数据得出变化规律,进而得出答案.
解答 解:∵(1)$\sqrt{2+\frac{2}{3}}$=$2\sqrt{\frac{2}{3}}$;
(2)$\sqrt{3+\frac{3}{8}}$=$3\sqrt{\frac{3}{8}}$;
(3)$\sqrt{4+\frac{4}{15}}$=$4\sqrt{\frac{4}{15}}$;
(4)$\sqrt{5+\frac{5}{24}}=5\sqrt{\frac{4}{25}}$
∴用含有n(n是正整数,且n>1)的代数式将规律表示出来为:$\sqrt{a+\frac{a}{{a}^{2}-1}}$=a$\sqrt{\frac{a}{{a}^{2}-1}}$.
故答案为:$\sqrt{a+\frac{a}{{a}^{2}-1}}$=a$\sqrt{\frac{a}{{a}^{2}-1}}$.
点评 此题主要考查了二次根式的性质与化简,正确得出数字之间变化规律是解题关键.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
20.y=-x2+(2-a)x+$\frac{9}{4}$是关于x的二次函数,当x的取值范围是1≤x≤5时,y在x=1时取得最大值,则实数a的取值范围是( )
| A. | a≥0 | B. | a≤1 | C. | 0≤a≤1 | D. | a>1 |
7.下列各式中,能用平方差公因式分解的是( )
| A. | x2+x | B. | x2+8x+16 | C. | x2+4 | D. | x2-1 |
17.有A,B两粒质地均匀的正方体骰子(骰子每个面上的点数分别为1,2,3,4,5,6),小王掷A,朝上的数字记作x;小张掷B,朝上的数字记作y.在平面坐标系中有一矩形,四个点的坐标分别为(0,0),(6,0),(6,4)和(0,4),小王小张各掷一次所确定的点P(x,y)落在矩形内(不含矩形的边)的概率是( )
| A. | $\frac{2}{3}$ | B. | $\frac{5}{12}$ | C. | $\frac{1}{2}$ | D. | $\frac{7}{12}$ |
4.有一种美丽的图形,它具有独特的对称美,有无数条对称轴,这种图形是( )
| A. | 等边三角形 | B. | 正方形 | C. | 正六边形 | D. | 圆 |
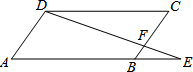 如图,E是?ABCD边AB延长线上的一点,AB=4BE,连接DE交BC于点F,则△DCF与四边形ABFD面积的比是$\frac{2}{3}$.
如图,E是?ABCD边AB延长线上的一点,AB=4BE,连接DE交BC于点F,则△DCF与四边形ABFD面积的比是$\frac{2}{3}$.