题目内容
3. 阅读理解:对于任意正实数a,b,因为($\sqrt{a}$-$\sqrt{b}$)2≥0,∴a-2$\sqrt{ab}$+b≥0,∴a+b≥2$\sqrt{ab}$,当且仅当a=b时,等号成立.结论:在a+b≥2$\sqrt{ab}$(a,b均为正实数)中,若ab为定值p,则a+b≥2$\sqrt{p}$,当且仅当a=b时,a+b有最小值2$\sqrt{p}$.
阅读理解:对于任意正实数a,b,因为($\sqrt{a}$-$\sqrt{b}$)2≥0,∴a-2$\sqrt{ab}$+b≥0,∴a+b≥2$\sqrt{ab}$,当且仅当a=b时,等号成立.结论:在a+b≥2$\sqrt{ab}$(a,b均为正实数)中,若ab为定值p,则a+b≥2$\sqrt{p}$,当且仅当a=b时,a+b有最小值2$\sqrt{p}$.根据上述内容,回答下列问题:
(1)若x>0,只有当x=2时,x+$\frac{4}{x}$有最小值4;
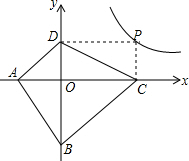
(2)探索应用:如图,已知A(-2,0),B(0,-3),点P为双曲线y=$\frac{6}{x}$(x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
分析 (1)根据题目所给信息可知x+$\frac{4}{x}$≥2$\sqrt{x•\frac{4}{x}}$,且当x=$\frac{4}{x}$时等号成立,可得出答案;
(2)可设P(x,y),可表示出四边形ABCD的面积为S四边形ABCD=6+$\frac{3}{2}x+y$,再利用所给信息可得到其最小值,此时x=2,y=3,可得出AC=BD,可得出四边形ABCD为菱形.
解答 解:
(1)由题目信息可知x+$\frac{4}{x}$≥2$\sqrt{x•\frac{4}{x}}$,且当x=$\frac{4}{x}$时等号成立,
∴当x=2时,x+$\frac{4}{x}$≥4,
即当x=2时,x+$\frac{4}{x}$有最小值4,
故答案为:2;4;
(2)设P(x,y)(x>0),则xy=6,
∵A(-2,0),B(0,-3),
∴AC=x+2,BD=y+3,
∴S四边形ABCD=$\frac{1}{2}$AC•BD=$\frac{1}{2}$(x+2)(y+3)=$\frac{1}{2}$(xy+3x+2y+6)=6+$\frac{3}{2}$x+y,
∵x>0,y>0,
∴$\frac{3}{2}$x+y≥2$\sqrt{\frac{3}{2}xy}$=2×$\sqrt{\frac{3}{2}×6}$=6,且当$\frac{3}{2}x$=y时等号成立,
∴当x=2,y=3时,$\frac{3}{2}$x+y有最小值6,
∴当x=2,y=3时,S四边形ABCD有最小值6+6=12,
当x=2,y=3时,AO=CO,BO=DO,且AC⊥BD,
∴四边形ABCD为菱形,
综上可知四边形ABCD的面积的最小值为12,此时四边形ABCD为菱形.
点评 本题主要考查反比例函数的综合应用,涉及反比例函数解析式、菱形的判定、四边形的面积等知识点和探究问题的能力.在(1)中关键是通过对题目信息的把握,把知识应用到题目的解决中来,在(2)中关键是设出P点坐标,用x、y把四边形ABCD的面积表示出来,再利用题目中的结论来解决.本题为阅读理解题,这类题目主要考查学生把握信息和处理信息的能力,难度不大.

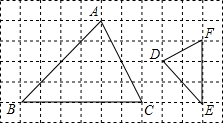 △ABC与△DEF在网格中的位置如图所示,如果每个小正方形的边长都是1.
△ABC与△DEF在网格中的位置如图所示,如果每个小正方形的边长都是1.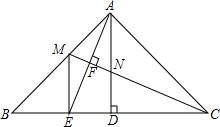 已知:如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E.CM⊥AE,垂足是F,交AD于N,交AB于M,连接ME.
已知:如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E.CM⊥AE,垂足是F,交AD于N,交AB于M,连接ME.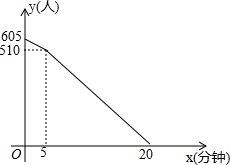 “五.一”假期,某火车客运站旅客流量明显增大,动车一般在开车前30分钟开始检票.假设某趟动车开始检票时已有605人到候车室排队检票,在检票开始5分钟内每分钟还有5个旅客进候车室进行检票,5分钟后到检票结束每分钟还会有2人到候车室排队检票,每分钟每个检票窗口检票12人(火车站会根据候车人数调研开放检票窗口数).此趟动车候车室排队等候检票的人数y(人)与检票时间x(分钟)的关系如图所示.根据关系图解答下列问题:
“五.一”假期,某火车客运站旅客流量明显增大,动车一般在开车前30分钟开始检票.假设某趟动车开始检票时已有605人到候车室排队检票,在检票开始5分钟内每分钟还有5个旅客进候车室进行检票,5分钟后到检票结束每分钟还会有2人到候车室排队检票,每分钟每个检票窗口检票12人(火车站会根据候车人数调研开放检票窗口数).此趟动车候车室排队等候检票的人数y(人)与检票时间x(分钟)的关系如图所示.根据关系图解答下列问题: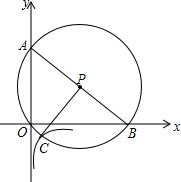 如图,在平面直角坐标系中,经过原点的圆P交坐标轴于点A,B,过点P作AB的垂线交圆P于点C,反比例函数y=$\frac{k}{x}$的图象经过点C.若OB-OA=4,则k的值为-4.
如图,在平面直角坐标系中,经过原点的圆P交坐标轴于点A,B,过点P作AB的垂线交圆P于点C,反比例函数y=$\frac{k}{x}$的图象经过点C.若OB-OA=4,则k的值为-4.